Topological solitonic excitations in charge density waves

Solitonic excitations with topological properties in charge density waves may be used as information carriers in novel types of information processing.

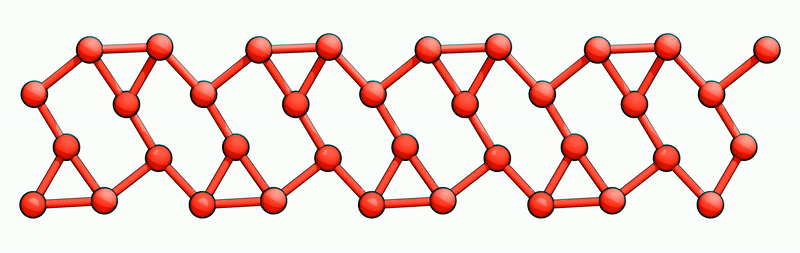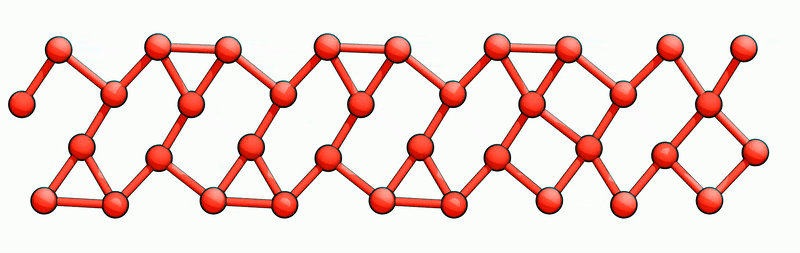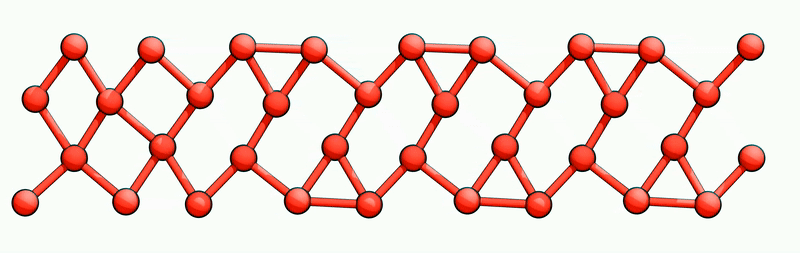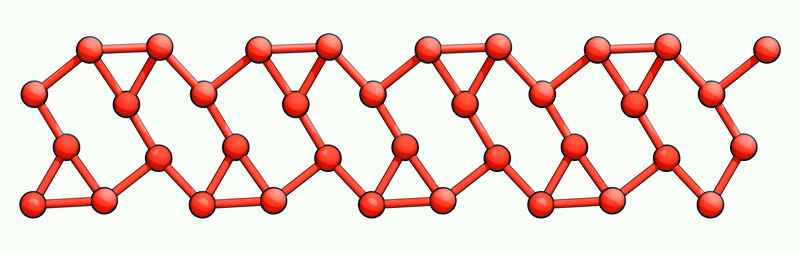
The Si(111)-(8x2)In atomic wire array is a prototypical model system for charge density wave (CDW) formation at surfaces. The CDW is created by a triple-band Peierls instability, driven by 3 soft phonon modes. Specific CDW states can be obtained directly from the phonon eigenvectors by coherent superposition of the original or inverted eigenvectors. Hence, 8 states are obtained in total, where 4 states are maxima on the potential energy surface and the other 4 states are ground states, respectively.

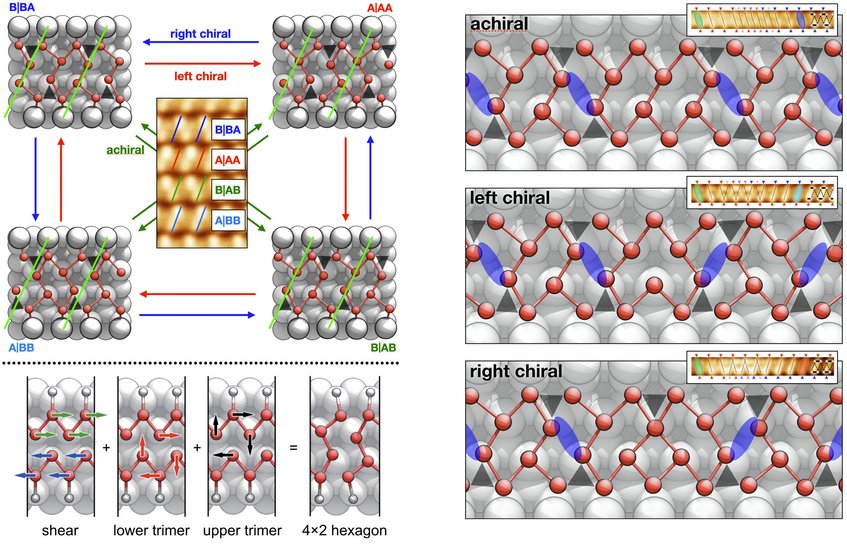
This 4-fold degenerate ground state allows us to form in total 12 different interfaces between any 2 ground states, cf. Fig. 1. The Si(111)-(8x2)In surface has a band inversion [SW et al., PRB 84, 115416 (2011)]. Symmetry arguments prove that these 12 interfaces must induce topological electronic states within the CDW bandgap and they can be grouped into 3 different "chiralities": (i) right chiral interfaces introduce a new occupied state into the band gap and are negatively charged; (ii) left chiral interfaces introduce a new empty state and are positively charged, whereas (iii) achiral interfaces are charge neutral.

Using our phonon expansion technique, we created the structures of all 12 interfaces from the phonon eigenvectors. To conveniently study these interfaces in experiments, they are frozen and trapped at adatom defects. The title image above shows a particular right chiral interface trapped at an In adatom defect. Our computed scanning tunneling microscopy (STM) images are in excellent agreement with STM measurements.

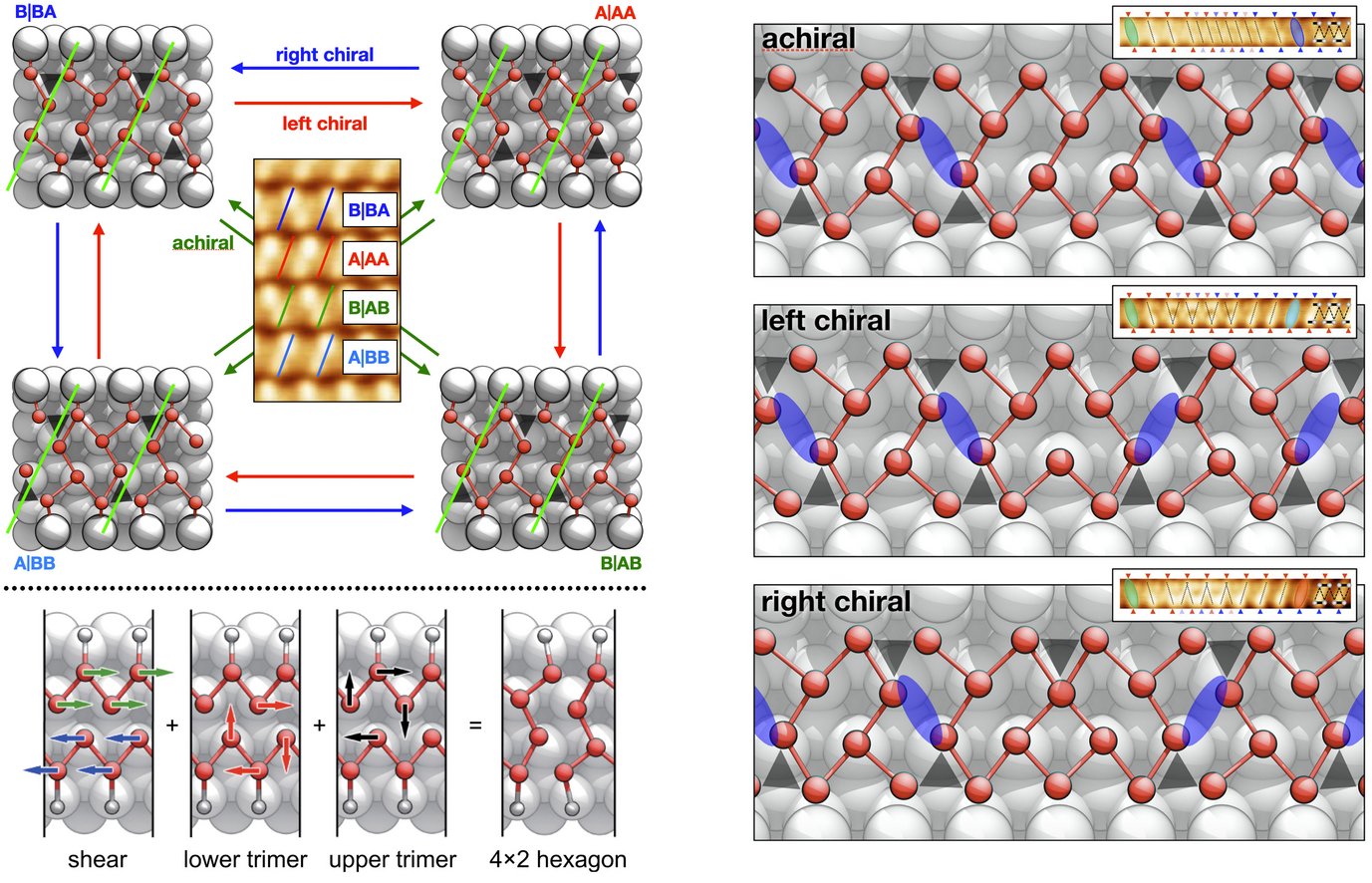
Fig. 1: 4 degenerate ground states can be interfaced in 12 different ways with 3 different chiralities. The lower panel illustrates the creation of the ground states by linear combination of phonon eigenvectors, shown here for the A|AA state. (B means inverting the associated eigenvector). On the right: 3 specific examples of chiral interfaces between degenerate ground states. — **Fig. 1:** 4 degenerate ground states can be interfaced in 12 different ways with 3 different chiralities. The lower panel illustrates the creation of the ground states by linear combination of phonon eigenvectors, shown here for the A|AA state. (B means inverting the associated eigenvector). On the right: 3 specific examples of chiral interfaces between degenerate ground states.

**Fig. 1:** 4 degenerate ground states can be interfaced in 12 different ways with 3 different chiralities. The lower panel illustrates the creation of the ground states by linear combination of phonon eigenvectors, shown here for the A|AA state. (B means inverting the associated eigenvector). On the right: 3 specific examples of chiral interfaces between degenerate ground states.

A particularly interesting property of these interfaces is that they can move as solitonic excitations through the wire. Within our phonon basis set, it is straight forward to show that in conjunction with the pure ground state the 3 different chiralities form a 4-element Abelian group, where the pure ground state is the neutral element and the achiral interface is the inverse element. Left and right chiral solitons are oppositely charged. Indeed, they can be pair-created from the pure ground state or undergo pair-annihilation. The achiral soliton, as the inverse element, transforms the right chiral soliton into the corresponding left chiral one and vice versa.

Furthermore, the solitons enable electron transport for excitation energies below the band gap by sliding the CDW as a whole. Starting, e. g., from state A|AA, transporting a right chiral soliton (RCS) through the wire from the right to the left will transform the wire into state B|BA. In the same manner, the next RCS then transforms B|BA -> A|BB and so on, as indicated by the blue arrows in Fig. 1. After 4 RCS in total, state A|AA is recovered. This process, however, has translated the CDW as a whole by exactly one (4x2) lattice constant to the left. Fig. 2 shows an animation of this process. Analogously, left chiral solitons traveling again from the right to the left perform hole transport and will translate the CDW to the right. Consistently with being uncharged, achiral solitons only invert the CDW phase but cannot perform any translation. Thus, they do not support any charge transport.

Fig. 2: Chiral transport by circular evolution. Initially, the wire is in state A|AA. Transporting a right chiral soliton (RCS) through the wire from the right to the left transforms the wire into state B|BA. The next RCS then switches the state to A|BB and so on. Completing the cycle, as indicated by the blue arrows in Fig. 1, returns the wire to the original state A|AA. The charge density wave, however, has undergone translation by one (4x2) lattice constant. — **Fig. 2:** Chiral transport by circular evolution. Initially, the wire is in state A|AA. Transporting a right chiral soliton (RCS) through the wire from the right to the left transforms the wire into state B|BA. The next RCS then switches the state to A|BB and so on. Completing the cycle, as indicated by the blue arrows in Fig. 1, returns the wire to the original state A|AA. The charge density wave, however, has undergone translation by one (4x2) lattice constant.

**Fig. 2:** Chiral transport by circular evolution. Initially, the wire is in state A|AA. Transporting a right chiral soliton (RCS) through the wire from the right to the left transforms the wire into state B|BA. The next RCS then switches the state to A|BB and so on. Completing the cycle, as indicated by the blue arrows in Fig. 1, returns the wire to the original state A|AA. The charge density wave, however, has undergone translation by one (4x2) lattice constant.

Note that soliton transport and interactions are most easily understood using the phonon eigenvectors as a basis set. In fact, the solitons can be seen as collective 2-phonon excitations. Dispersion is prevented by a strongly non-linear phonon-phonon interaction: interactions other than the ones described above involve transitions across the 4 energy barriers described in the first paragraph, which are effectively forbidden.

Moreover, the 3 phonons that both drive the phase transition and the soliton formation exhibit strong electron-phonon coupling. As shown in our ultrafast dynamics project, they can be excited optically. In analogy to concepts from femtochemistry, we propose that the solitons can be optically excited and controlled by fs laser pulse sequences. To this purpose, we are currently performing constrained density-functional molecular dynamics simulations on the excited state potential energy surface.

Topological solitonic excitations in charge density waves

Metal to charge density wave interfaces

Ultrafast dynamics in charge density waves

Topological solitonic excitations in charge density waves

Other Interesting Articles