Thermopotentiostats for molecular dynamics

It is very challenging to simulate electron-transfer reactions under potential control within high-level electronic structure theory, e. g. to study electrochemical and electrocatalytic reaction mechanisms. We develop a novel method to sample the canonical NVTΦ or NpTΦ ensemble at constant electrode potential in ab initio molecular dynamics simulations. Our approach is general and can be applied with any standard density-functional simulation package.

Molecular dynamics has become an indispensible tool to efficiently simulate the behaviour of macroscopic systems, using models with finite size and reduced complexity. At finite size, however, intensive quantities, that are controlled at the macroscale, are no longer constant but fluctuating. These local fluctuations impact kinetics significantly and must be taken into account explicitly in finite simulation cells. They are inherent to any thermodynamic degree of freedom, including the pressure and electric potential. Thus, potentiostats must allow for explicit temperature fluctuations in the applied electric field, and hence become thermopotentiostats.

Any valid thermopotentiostat must solve three critical problems:

1. Without potential control, any internal process that changes the total polarization leads to a persistent change in the effective field experienced by the system afterwards, and hence to a different evolution.
2. Without thermal fluctuations, a potentiostat systematically cools the electrically active degrees of freedom, creating an artificial thermal imbalance.
3. If the power spectrum of a thermopotentiostat's fluctuations is not balanced against the energy dissipation from potential control, such a thermopotentiostat creates a thermal imbalance within the spectrum of the internal degrees of freedom.

For the first time, we solve all three problems simultaneously and introduce a novel thermopotentiostat, which is the electric equivalent to the Langevin thermostat.

Straightforward approaches to adjust the potential with a relaxation time are always dissipative. These are conceptually similar to the Berendsen thermostat, which adjusts the kinetic energy with a relaxation time. It suffers from a simulation artefact known as the flying ice cube effect. As it dissipates the difference between the instantaneous and mean kinetic energy, it dissipates temperature fluctuations until the instantaneous kinetic energy becomes constant. As a result, all particles eventually share the same velocity. In resemblance of the Maxwell demon, disordered thermal motion has been converted into ordered translational motion. Analogously, direct potential control schemes dissipate thermally induced potential fluctuations.

Therefore, energy dissipated by the deterministic potential control must be balanced, on average, to energy gained from stochastic thermal fluctuations. The potential control mechanism effectively introduces a resistance. Johnson and Nyquist recognized that a resistor on a transmission line creates electric fluctuations at its leads. This is analogous to the radiation resistance seen by an oscillating electric dipole in free space, giving rise to a fluctuating electric field as described by Planck's radiation law. Based on stochastic differential equations and Ito calculus, we derived a formally exact thermopotentiostat from fundamental thermodynamics and the fluctuation dissipation theorem. Even in absence of a thermostat, the fluctuating electric field of our thermopotentiostat will correctly thermostat the system. Enabling full dynamic potential control, it is a necessary prerequisite for simulating processes rather than only thermodynamic equilibrium.

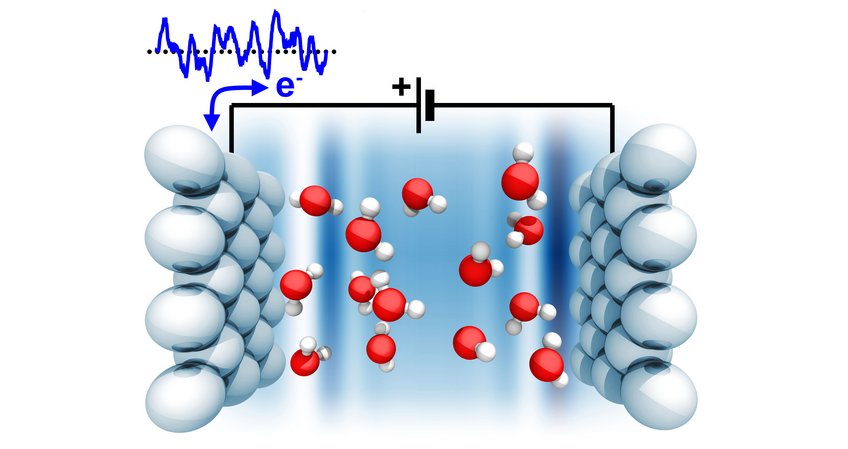
As a first application, we performed simulations of the interfacial dielectric properties of liquid water by applying a voltage using our thermopotentiostat. Close to the interface, the inverse dielectric constant of water exhibits negative values (overscreening) and approaches its bulk value in an oscillatory fashion. This behaviour reflects the finite size of the water molecules and the inherent non-locality of water's dielectric constant. It is reminiscent of Friedel oscillations, where the finite size of the electron - its wavelength - determines the dielectric screening behaviour and the wavelength of the oscillations.

At present, we are developing a generalized, more advanced control scheme and implement our methods in ab initio electronic structure codes.