Uncertainty Propagation for Density Functional Theory
While Density Functional Theory (DFT) is in principle exact, the exchange functional remains unknown, which limits the accuracy of DFT simulation. Still, in addition to the accuracy of the exchange functional, the quality of material properties calculated with DFT is also restricted by the choice of finite bases sets.
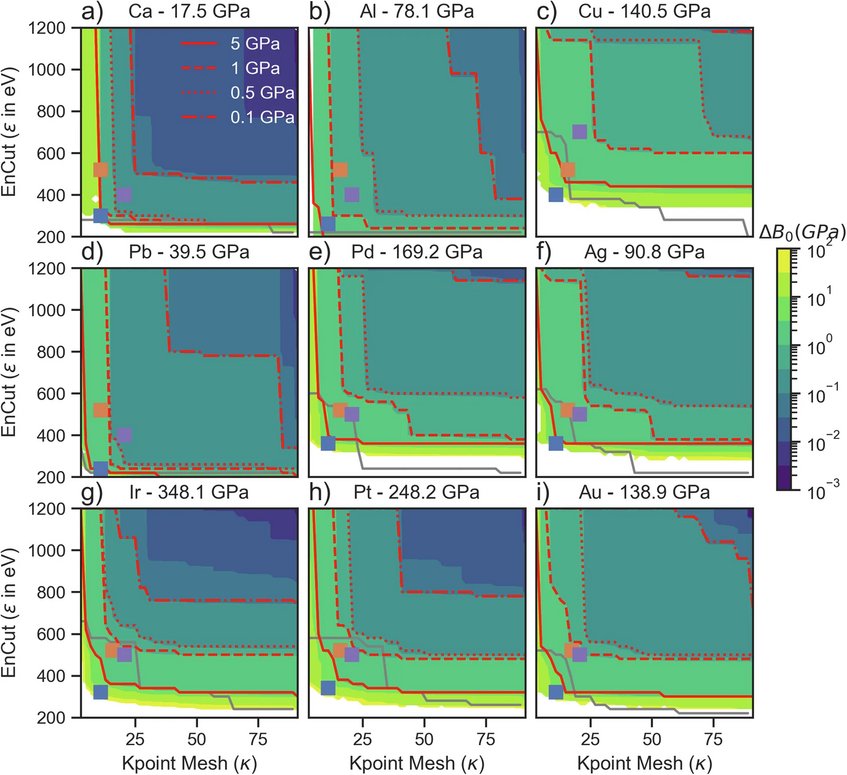
For the case of plane-wave DFT these bases sets are the reciprocal k-point mesh and the plane-wave energy cut-off. Given that the total number of plane waves to represent the Potential Energy Surface (PES) depends on both the plane wave energy cut-off and the k-point mesh density, it is insufficient to converge both parameters independently. For studying the convergence of a material property like the bulk modulus, it is recommended to visualize it over a contour plot with the k-point mesh on the x-axis and the plane wave energy cut-off on the y-axis. In Figure 1. the difference in the bulk modulus at a finite set of convergence parameters in comparison to the bulk modulus at the maximum convergence parameters is plotted as uncertainty for nine elements.
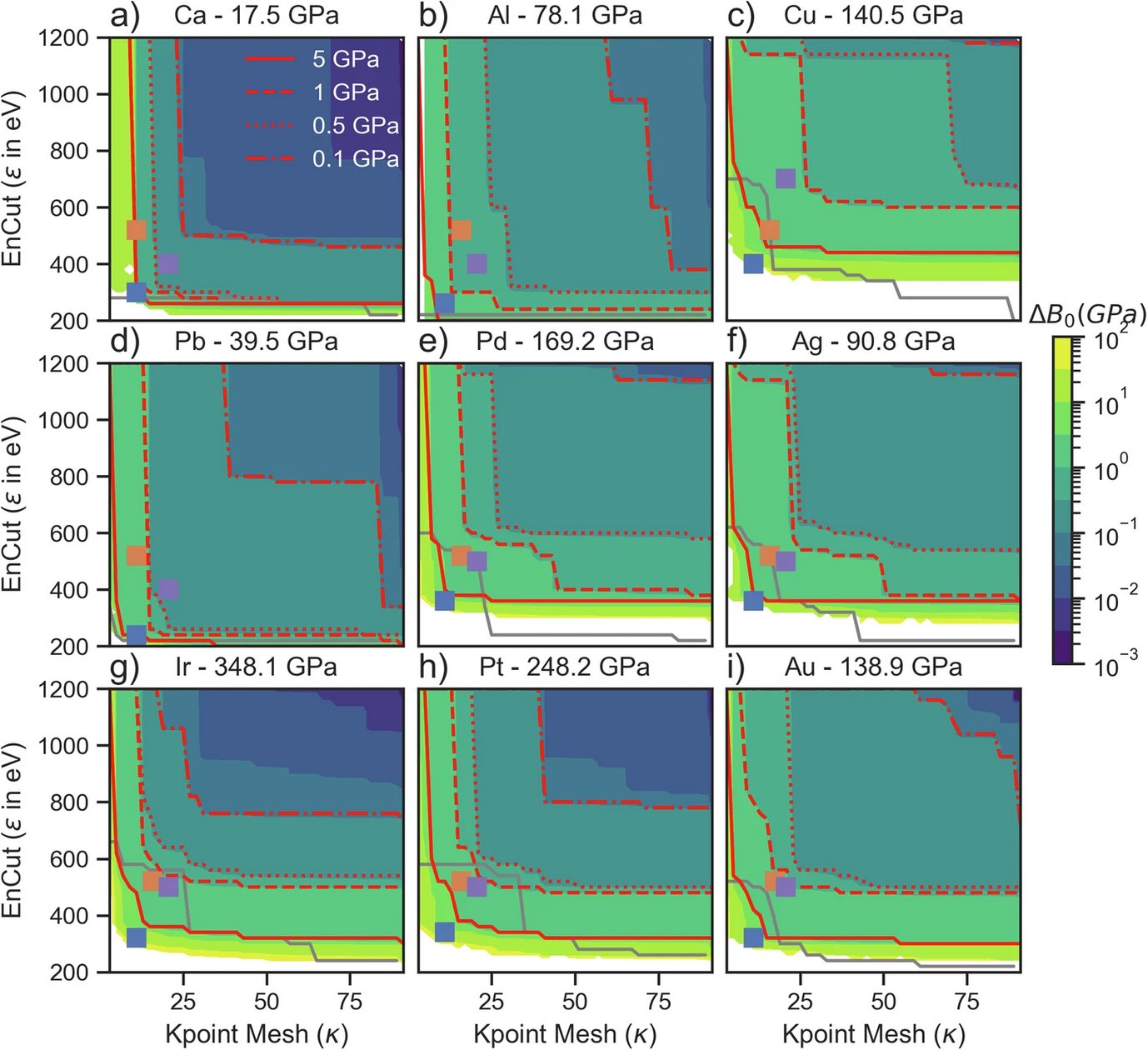
These extensive studies of the convergence of the bulk modulus in dependence to the k-point mesh density and the plane wave energy cut-off require over 50 000 individual DFT simulation. This challenge can be addressed by applying tensor decomposition on the convergence dataset. The tensor decomposition highlights, two primary components, one for the k-point mesh density and one for the plane wave energy cut-off. Consequently, the uncertainty in the bulk modulus can be divided into two systematic contributions, again one for the k-point mesh density and one for the plane wave energy cut-off and a statistical contribution. The three contributions to the uncertainty can be predicted based on a subset of DFT simulation. Only 5 000 DFT calculations are required, to approximate the convergence of the uncertainty in dependence of the k-point mesh density and plane wave energy cut-off.
This study was enabled by the high-throughput screening capabilities of the pyiron workflow framework and the optimized workflow to approximate the uncertainty over the whole parameter space with just 10% of the simulation is also implemented in the pyiron workflow framework. This data-driven approach to method development in materials science, based on generating large datasets, deriving coarse-grained models and up-scaling these coarse-grained models to apply them in high-throughput screening studies is a key methodology in the field of materials informatics.