Ab initio up to the melting point: Anharmonicity and vacancies in aluminum

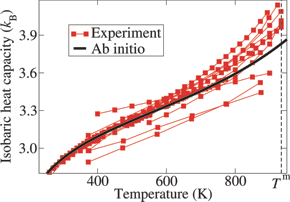
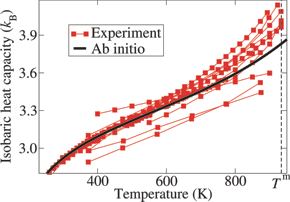
The balance between different contributions to the high-temperature heat capacity of materials can hardly be assessed experimentally. In this study, we develop computationally highly efficient ab initio methods which allow us to gain insight into the relevant physical mechanisms. Some of the results have lead to breakdown of the common interpretation of temperature dependencies.

High-temperature isobaric heat capacity of aluminum from experiment and ab initio calculations. The melting temperature of aluminum, 933 K, is denoted by Tm and the Boltzmann constant by kB.

At elevated temperatures, the heat capacity of metals significantly deviates from the behavior predicted within the perfect harmonic lattice model. This was pointed out already in 1921 in a seminal work by Born and Brody [1]. In this and in many subsequent studies, various mechanisms have been proposed to explain these deviations. Only recently, our ab initio calculations for a wide range of non-magnetic metals showed that the predominant part of these deviations can be explained on the basis of quasiharmonic (going beyond linear Grüneisen theory) and electronic excitations (see Ref. [2] and the discussion here). A generalization to magnetic systems was given in Ref. [3] and is also discussed here. However, the subtle balance between further contributions, in particular explicit anharmonicity (see below for definition) and vacancies, could not be clarified yet even for simple elementary metals. [4]

Research projects in Computational Phase Studies

Other Interesting Articles

Web-View
Print Page
Open in new window
Estimated DIN-A4 page-width
Go to Editor View