Quasi-Newton Transition State Optimization
In order to estimate the kinetics of thermally activated processes, one must determine the energy of the transition state. This transition state is a first-order saddle point on the potential energy surface, i.e., it is a maximum along the reaction coordinate, but a minimum with respect to all other directions in configurational space. We have developed an efficient Quasi-Newton algorithm to optimize the structure of the transition state.

In Quasi-Newton schemes, the atomic forces are minimized by ussing the Hesse matrix (Hessian) that describes how forces change upon small displacements of the atoms. Computing the Hesse matrix directly is very costly. Therefore, one replaces the exact Hessian by a guess that is then improved iteratively based on the force changes in the previous steps.
Our approach builds upon our on-the-fly fitting of a simplified model for the initial Hessian developed for energy minimization [1], namely a bond-stretching model (and optional angular terms) that is automatically generated from the atomic positions. This approach is also known as redundant internal coordinates, and in its naive implementation has a huge number of unknown force constants. To minimize the number of free parameters, all bonds are therefore typified according to bond length and chemical species, and all bonds of the same type are then treated as equal. This allows to determine all the parameters from a few displacements only, often only a single one. This initial model gives a qualitatively correct picture of the Hessian that is much better than the commonly applied diagonal in the optimization coordinates, and thus also needs fewer corrections by subsequent optimization steps.
In energy minimization, we enforce a positive definite Hessian by making all force constants positive and using Broyden-Fletcher-Goldfarb-Shanno (BFGS) updates. For transition state optimization, the challenge is to identify the reaction coordinate, and ensure it maintains a negative curvature only along this direction. While there is no general solution to this problem, we very often have a reasonable guess of the direction of the transition coordinate at the barrier. For instance, if we know the initial and final minimum structure, we could use the linear interpolation of atomic positions to estimate the direction of the transition coordinate in configurational space. Even if this is not perfect, it will be sufficient to make reasonable first steps. As the optimization proceeds, we monitor the eigenvalues and eigenvectors of the updated Hessian to identify and maintain the best guess for the negative-curvature direction.
Thus, the algorithm proceeds as follows. First, the bond-stretching (and possible angle-deformation) model is parametrized enforcing a Hessian with non-negative eigenvalues (positive semi-definite). This Hessian is then corrected along the current guess for the reaction coordinate direction in Cartesian coordinates using Murtagh-Sargent updates to enforce a negative curvature. Then, the Hessian updates are made in Cartesian coordinates using the force-displacement relationships from the previous steps. The resulting Hessian is then diagonalized (yielding the spectral representation of eigenvalues and eigenvectors) and analyzed. If the Hessian has exactly one negative eigenvalue, the corresponding eigenvector is used to update the transition coordinate direction for future steps. If there is no negative eigenvalue, the Murtagh-Sargent update for the transition direction is repeated to ensure a energy maximization along this direction. If there are two or more negative directions, the curvature in the negative subspace is corrected by inverting the components that are orthogonal to the current guess of the transition direction. The spectral representation is also used to limit step-sizes in a meaningful manner, namely by minimizing the predicted force while constraining the total step length.
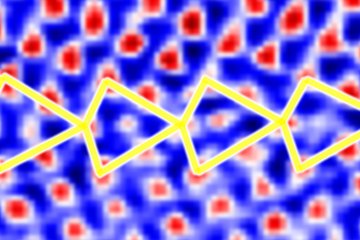
The algorithm was implemented in the SPHInX code (available as ricTS structure optimizer). It was tested and used for determining field evaporation paths from Al surfaces in the vicinity of a grain boundary (see image). It takes a comparable number of steps as the energy minimization (usually 10-30 force evaluations, depending on the quality of the initial structure). This makes it significantly more efficient for transition barriers than nudged-elastic band (NEB) approaches for the same task. Of course, NEB yields additional points on the minimum energy path that may be useful for further investigations beyond the kinetic barriers. Yet, when the focus is on barrier computation for reasonably well-defined reaction paths, our direct optimization of the transition state is ideally suited.