Orbital Contrast in Field Ion Microscopy
We simulate the ionization contrast in field ion microscopy arising from the electronic structure of the imaged surface. For this density-functional theory (DFT) calculations of the electrified surface are combined with the Tersoff-Hamann approximation to electron tunneling. The approach allows to explain the chemical contrast observed for alloys.
Background: the field ion microscopy experiment
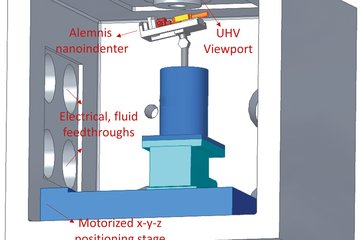
Field ion microscopy (FIM) is a relatively old technique to image surfaces with atomic resolution (and indeed the first ever experimental technique to achieve this). FIM has been a Sleeping Beauty until recently, when people realized that it complements atom probe tomography (APT) by resolving crystallographic defects such as dislocations, and can be carried out in the same experimental setup (read more...). In FIM (as well as in APT), a needle-shaped specimen of about 100 nm diameter is cut out from the sample of interest and subject to a high voltage. In FIM, the extreme electric field at the tip surface (several 10 V/nm) allows to ionize gas atoms close to the surface. These ions then fly off towards the counter electrode along the field lines and hit a screen (or nowadays a position-sensitive electronic detector) where they produce an image of the surface or in fact an image of the ionization probability above the surface. (In APT, it is the surface atoms themselves that get ionized). For carefully selected field strengths (best imaging field), the resolution can image single atoms on the surface, which appear as spots in the FIM image. The brightness of the spots varies over the surface due to both variations in the local field strength and differences in the electronic structure (e.g. when different chemical species are present). Field ion microscopy by itself cannot identify the origin of brightness variations in the image, but the relative positions reveals the underlying crystallographic structure.
New insights by DFT-based simulations.
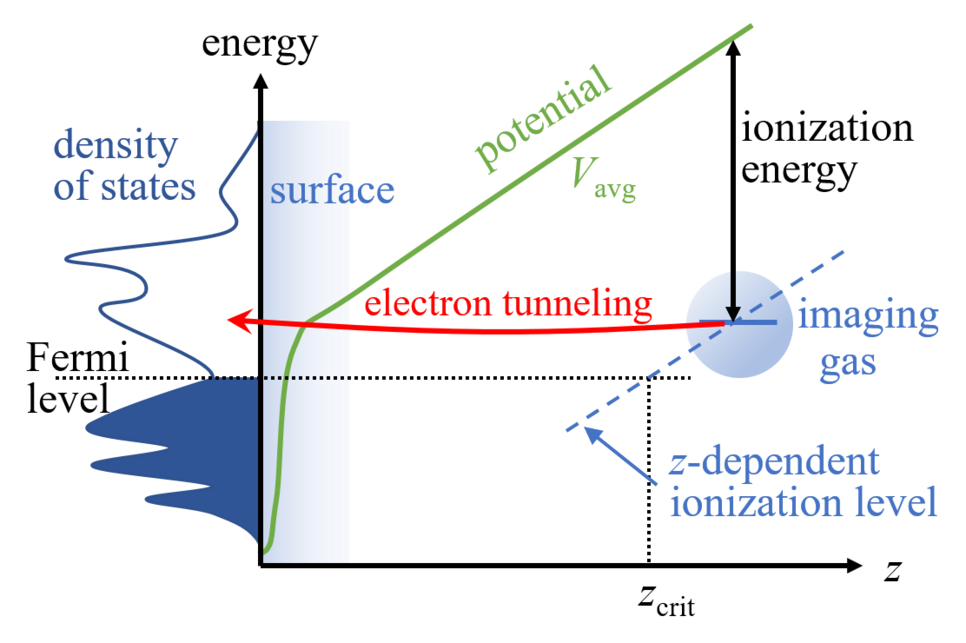
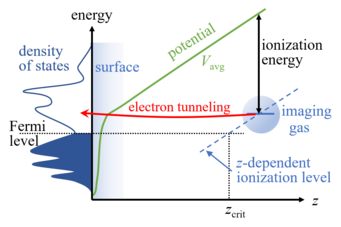
In order to better understand the influence of the electronic structure, notably chemical contrast occasionally observed in FIM and corroborated by correlative APT-FIM experiments, we perform DFT simulations. For describing a surface in the presence of the electric field, we use our recently developed generalized dipole correction. The ionization of the imaging gas (He, Ne) above the surface requires that an electron tunnels from the rare gas atom into empty states of the surface, see the sketch. This is only possible if the ionization energy (on the order of 20 eV) is counter-balanced by the voltage drop between the rare gas ion and the surface, i.e., the gas atom must be a 0.4-1 nm above the surface. The tunneling probability can be estimated from the Tersoff-Hamann approximation, originally developed for the interpretation of scanning tunneling microscopy. In this approximation, the tunneling probability is proportional to the surface local density of states at the position of the rare gas ion.
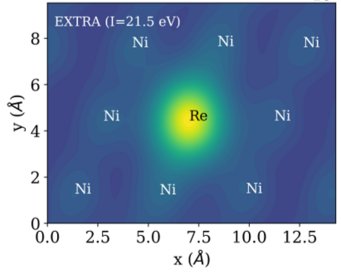
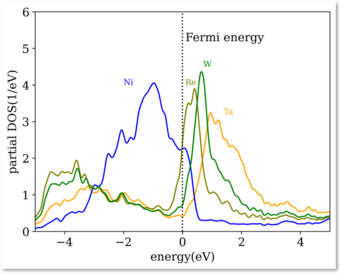
The theory has been used successfully to explain the bright appearance of Ta, W, and Re alloying elements in Ni-based super-alloys. The origin of this chemical contrast lies in the different number of empty d-states. Ni, being a late transition metal, has an almost filled d-band. Elements to the left in the periodic table have fewer d-electrons, and hence additional empty d-states slightly above the Fermi level that can receive the electron from the imaging gas.
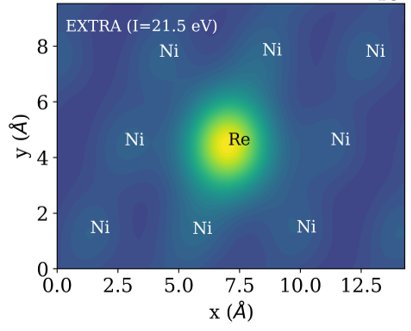
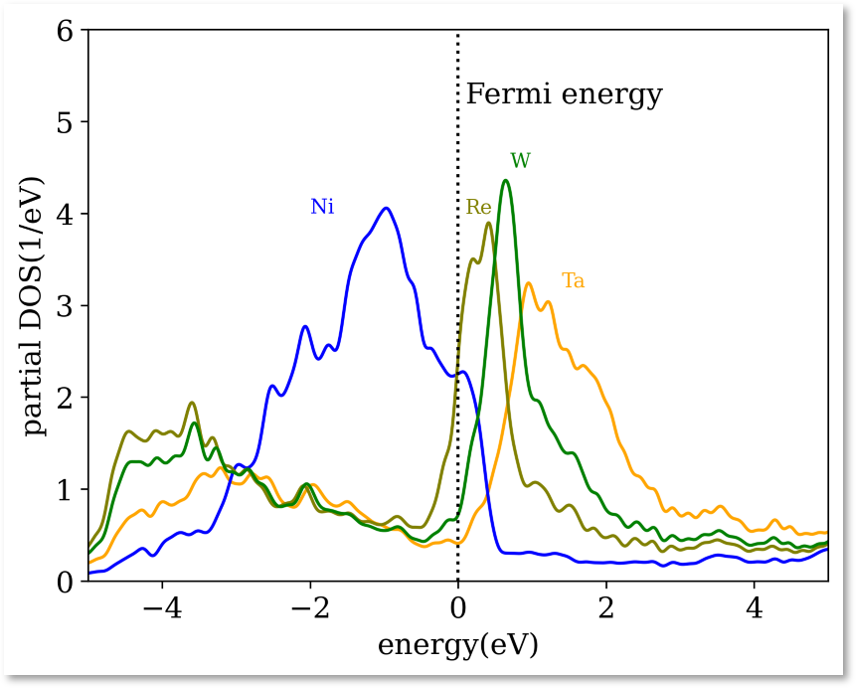
The EXTRA extrapolation algorithm
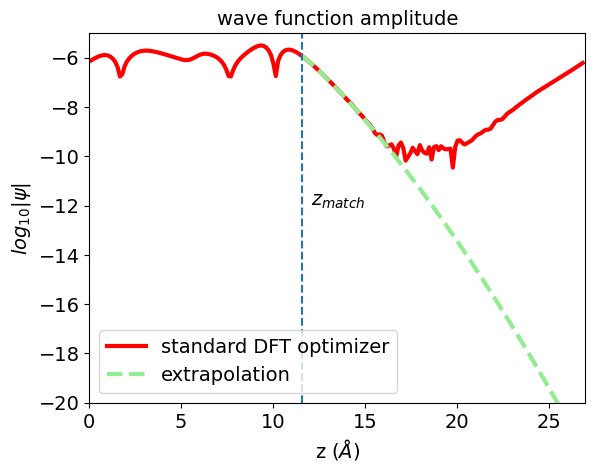
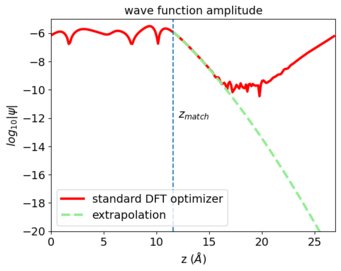
A major challenge in these calculations turns out to be the rapid decay of the empty surface states into which the electrons from the imaging gas may tunnel. At the distance where the tunneling takes place, the wavefunctions are 6-12 orders of magnitude smaller than their maximum value near the surface. The numerically computed values obtained from standard DFT calculations are therefore strongly affected by numerical noise (as visible from the wave function profile), because the underlying algorithms perform a global optimization and treat small-value regions as unimportant. To address the issue, we have developed a tail extrapolation algorithm that works at local scale, i.e., which can intrinsically deal with the predominant loss of amplitude along the surface normal. For one-dimensional problems, reverse Numerov integration and matching is a feasible solution. We generalized this algorithm to three dimensions, and combine it with an adaptive Fourier-filtering and preconditioning to obtain a numerically robust matching scheme. The EXTRA_FIM code is publicly available.
Application to ordered alloys
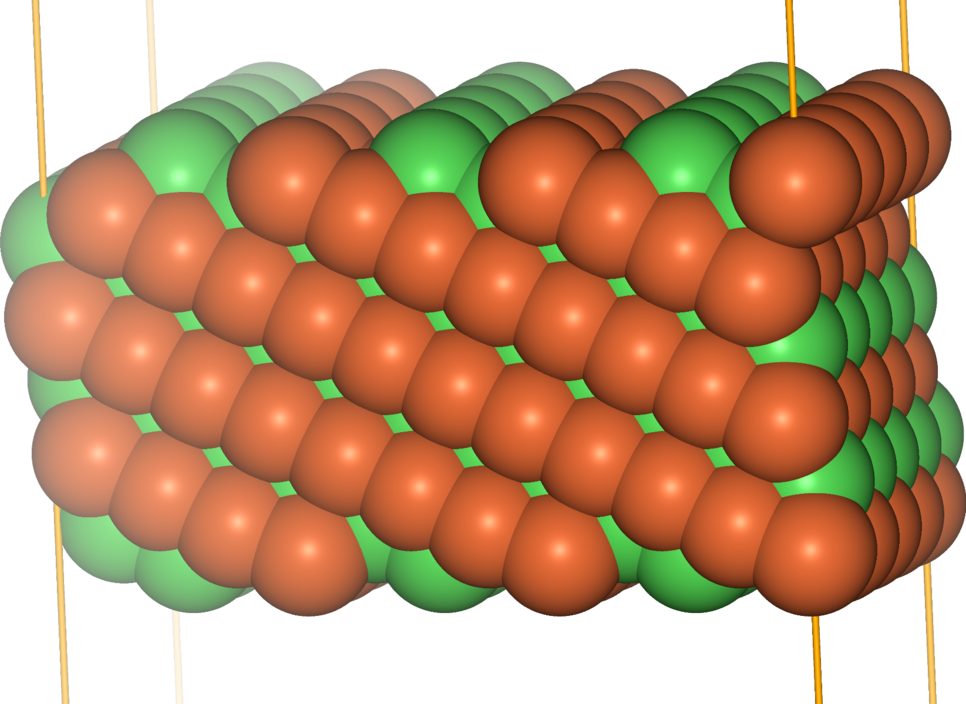
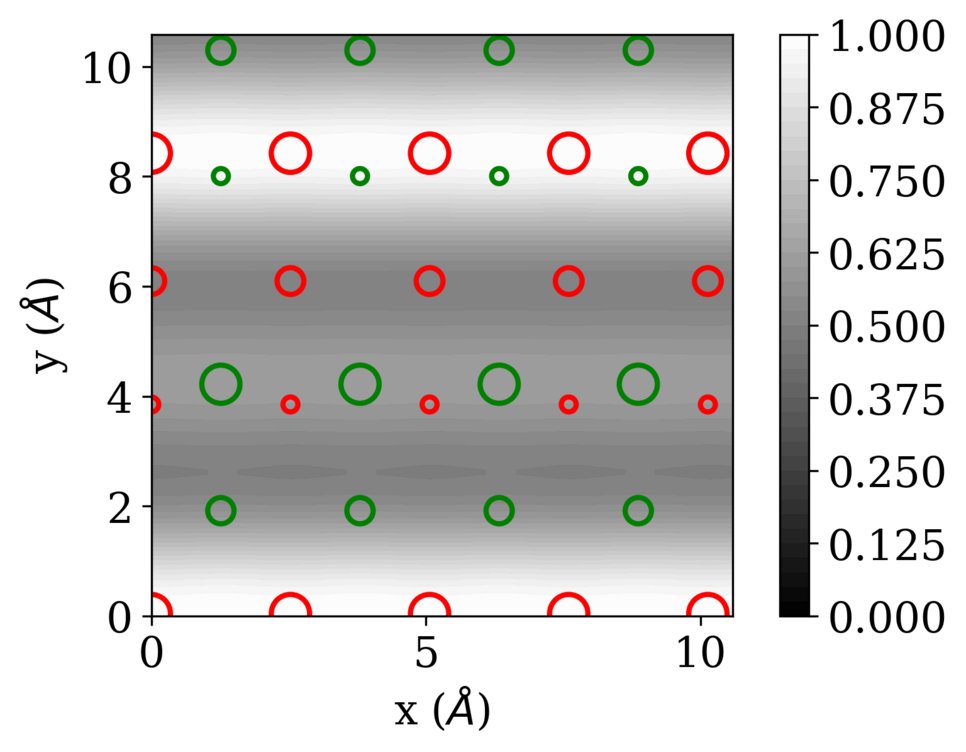
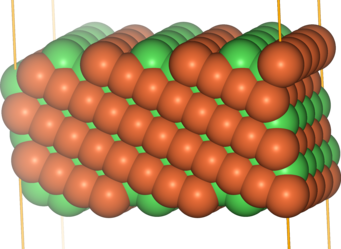
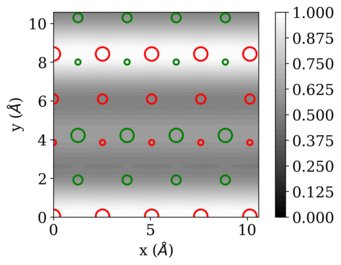
We have applied the approach to FeNi in the L10 ordering, which consists of alternating layers of Fe and Ni in an fcc structure. Also this ordered alloy shows chemical contrast in FIM, revealing the layered structure when the layers cut the surface plane. The figures below show the example of the FeNi (113) surface (with the layers stacked along the [001] direction).