Generalized Dipole Correction for Charged Slabs

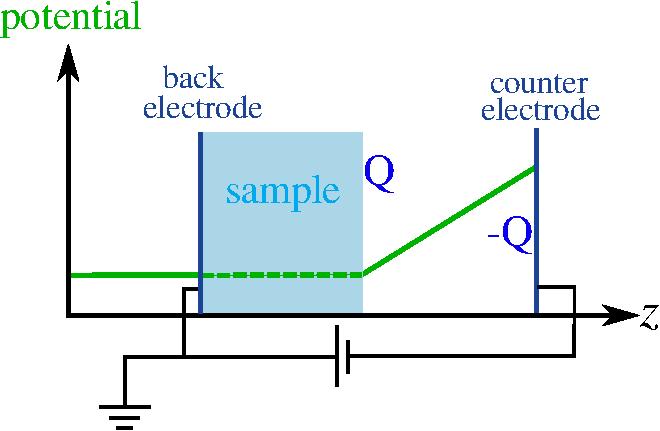
It is very challenging to simulate within DFT extreme electric fields (a few 10¹⁰ V/m) at a surface, e.g. for studying field evaporation, the key mechanism in atom probe tomography (APT). We have developed a straight-forward scheme to incorporate an ideal plate counter-electrode in a nominally charged repeated-slab calculation by means of a generalized dipole correction of the standard electrostatic potential obtained from fully periodic FFT.

Extreme electric fields (a few 10¹⁰ V/m) trigger field evaporation, the key mechanism in atom probe tomography (APT). When studying the elementary process at the APT tip surface by density-functional theory, the voltage drop across the simulation cell is a few 10 V, much larger than the typical energy scale of valence electrons. This precludes any attempts to generate the fields by real ions.

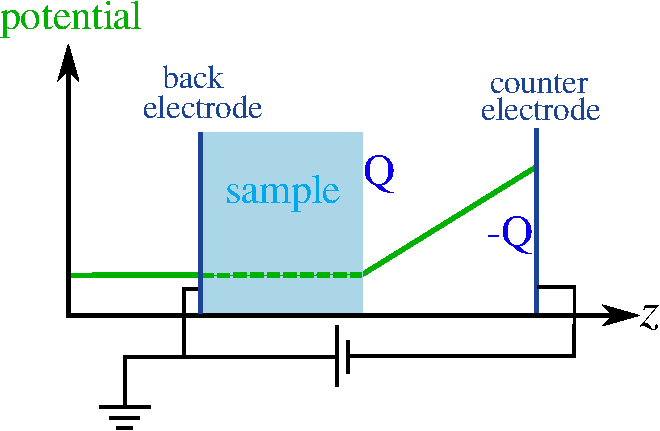
To address the challenge, we model the electrified surface by a charged slab in a periodic cell. By default, the counter charge is smeared out, which produces an uncontrollable distribution of the electric fields. Therefore, a counter electrode must be placed in the center of the vacuum region. Moreover, the field-induced potential drop can be accomodated by a discontinuity in the electrostatic potential, a technique now known as the "dipole correction" for asymmetric slabs We combined these two ideas into a single "generalized dipole correction". It accounts for the removal of the implict smeared-out counter charge, the placement of the (virtual) counter electrode, the discontinuity, and the consistent alignment of the resulting potential. Further improvements ensure a proper initialization and suppression of charge fluctuations, enabling surface calculations for fields even beyond the evaporation threshold.

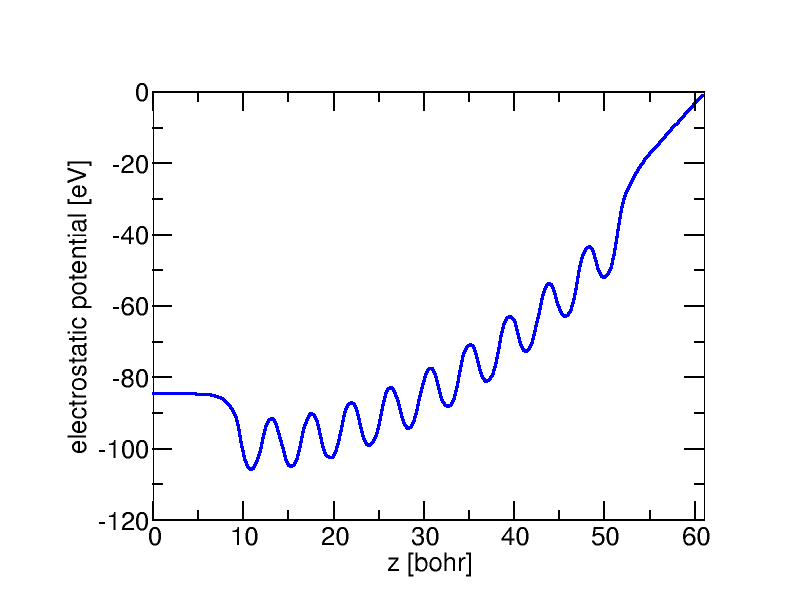
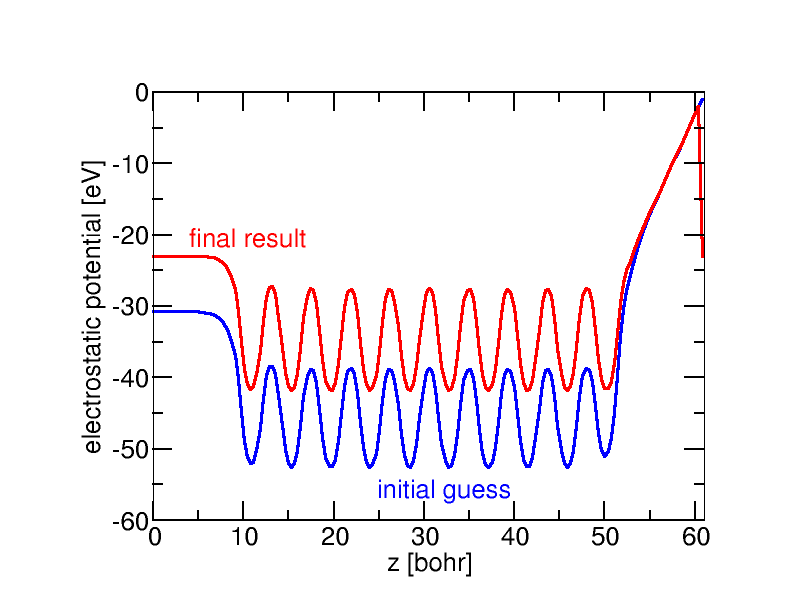
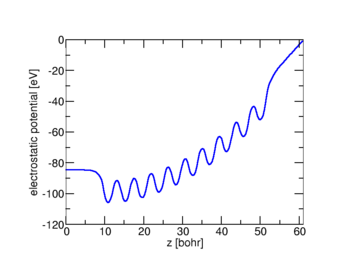
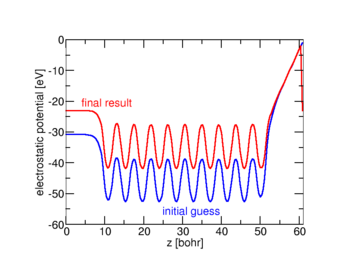
One of the challenges for actual calculations on charged slabs using the generalized dipole correction turned out to be the high sensitivity of the potential to incorrect distributions of the charge. This is particularly important for the very first step. Traditionally, initial guesses for charged systems were obtained by rescaling the electron density to obtain the desired norm. However, this smears out the extra charge over the entire slab instead of localizing it at the surface. In consequence, the electric field penetrates the inner of the slab and deforms the potential in dramatically (see upper left). By initializing with an extra sheet charge (or spherical Gaussian charges) close to the surface avoids this bad starting point (upper right).

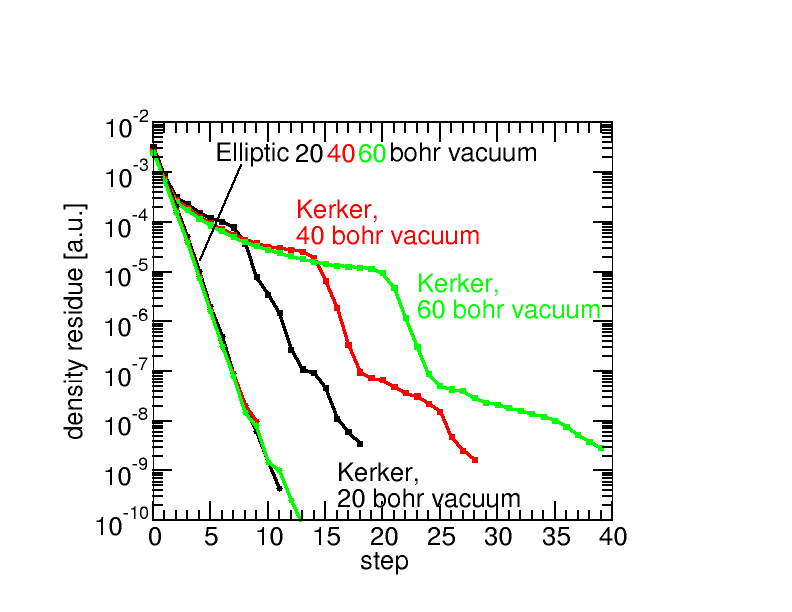
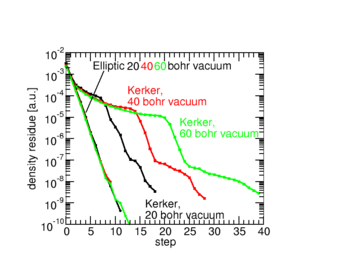
But charge fluctuations can also occur during the self-consistency iterations central to the DFT algorithm. These turned out to be problematic, the thicker the slab is and - surprisingly - the thicker the vacuum region between the slabs. The problem is already visible for charge-neutral slabs and results from the fact that screening in a metal-vacuum is very inhomogeneous. This inhomogeneity is not taken into account by common preconditioners. However, a very clever solution is to use an inhomogeneous preconditioner, that solves an elliptic partial differential equation. This "elliptic preconditioner"-idea was first proposed for potential-mixing (L. Lin and C. Yang, 2013), and we adapted it to density-mixing with great success.

Using the generalized dipole correction allows us to study the fundamental mechanism of field evaporation in greate detail. Apart from a direct proof of the roll-over effect (see left), we also obtain interesting results regarding the energetics (read more...)