Large scale forming simulation by using DAMASK-based crystal plasticity methods
Why is it important to consider metal anisotropy in forming simulations?
Anisotropy is the property of being directionally dependent, which implies different properties in different directions, as opposed to isotropy where the properties do not depend on direction.
It can be defined as a difference, when measured along different axes, in a material's physical or mechanical properties. In metals this effect is particularly pronounced as particularly their mechanical properties, such as Young's modulus, plastic flow, yield strength, tensile strength, toughness, ductility, damage and fracture as well as creep and diffusion, are often highly dependent on the direction of loading. This means that all these properties are tensor valued properties and not scalars. Just as an example all fourth rank tensor properties, like the elastic constants, are anisotropic, even for materials with cubic symmetry.
The Young's modulus relates stress and strain when an isotropic material is elastically deformed; to describe elasticity in an anisotropic material, stiffness (or compliance) tensors are used instead.
In metals, anisotropic elasticity behavior is prevalent in all single crystals, with the exception of Tungsten, due to the fact there are only two independent stiffness coefficients in the stiffness tensor (while other cubic crystals have three). For face centered cubic materials like Copper, the elastic modulus is highest along the <111> direction, normal to the close packed planes.
Spectral-based representative volume element crystal plasticity simulations to predict yield surface evolution during large scale forming simulations
By using the DAMASK simulation package we developed a new approach to predict the evolution of anisotropic yield functions by coupling large scale forming simulations directly with crystal plasticity-spectral based virtual experiments, realizing a multi-scale model for metal forming.
Employing a fast spectral method solver enables us to conduct on-the-fly full-field virtual experiments to evolve the yield surface at each integration point of the macroscopic finite element model. As illustrative example, two advanced anisotropic yield functions, namely Yld2000-2D and Yld2004-18p, are used in finite element simulations of deep drawing for a 2090-T3 aluminum alloy sheet. The simulated earing profiles are compared to the experimental ones as well as to simulations with non-evolving yield functions. It is found that the prediction of the earing is improved for the case of the evolving Yld2000-2D yield function. The evolution of the plastic anisotropy during cup drawing is systematically analyzed, showing that the evolution of anisotropy can have considerable effect on the prediction accuracy of the macroscopic simulations.
Microstructure-based multiscale modeling of large strain plastic deformation by coupling a full-field crystal plasticity-spectral solver with an implicit finite element solver
Another approach for combining the simulation of microstructure-based multiscale texture problems with large strain plastic deformation consists in coupling a full-field crystal plasticity-spectral solver with an implicit finite element solver.
For this purpose we developed a fully embedded implementation of a full-field crystal plasticity model in an implicit finite element (FE) framework, a combination which realizes a multiscale approach for the simulation of large strain plastic deformation. At each integration point of the macroscopic FE model a spectral solver, based on Fast Fourier Transforms (FFTs), feeds-in the homogenized response from an underlying full-field polycrystalline representative volume element (RVE) model which is solved by using a crystal plasticity constitutive formulation. Both, a phenomenological hardening law and a dislocation density based hardening model, implemented in the open source software DAMASK, have been employed to provide the constitutive response at the mesoscale. The accuracy of the FE-FFT model has been benchmarked by one-element tests of several loading scenarios for an FCC polycrystal including simple tension, simple compression, and simple shear. The multiscale model is applied to simulate four application cases, i.e., plane strain deformation of an FCC plate, compression of an FCC cylinder, four-point bending of HCP bars, and beam bending of a dual-phase steel. The excellent capabilities of the model to predict the microstructure evolution at the mesoscale and the mechanical responses at both macroscale and mesoscale are demonstrated.
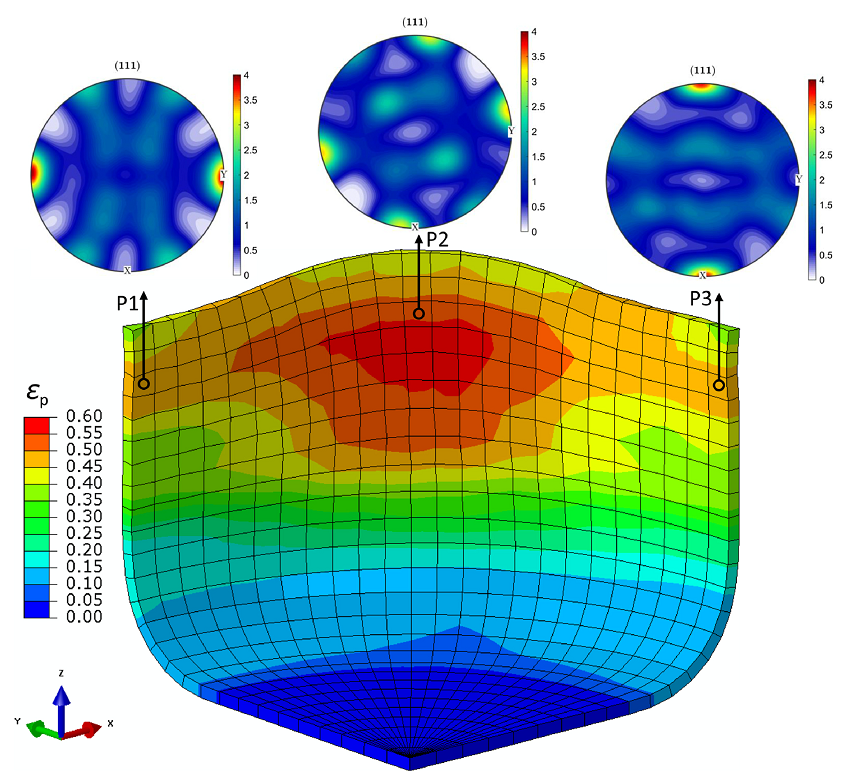
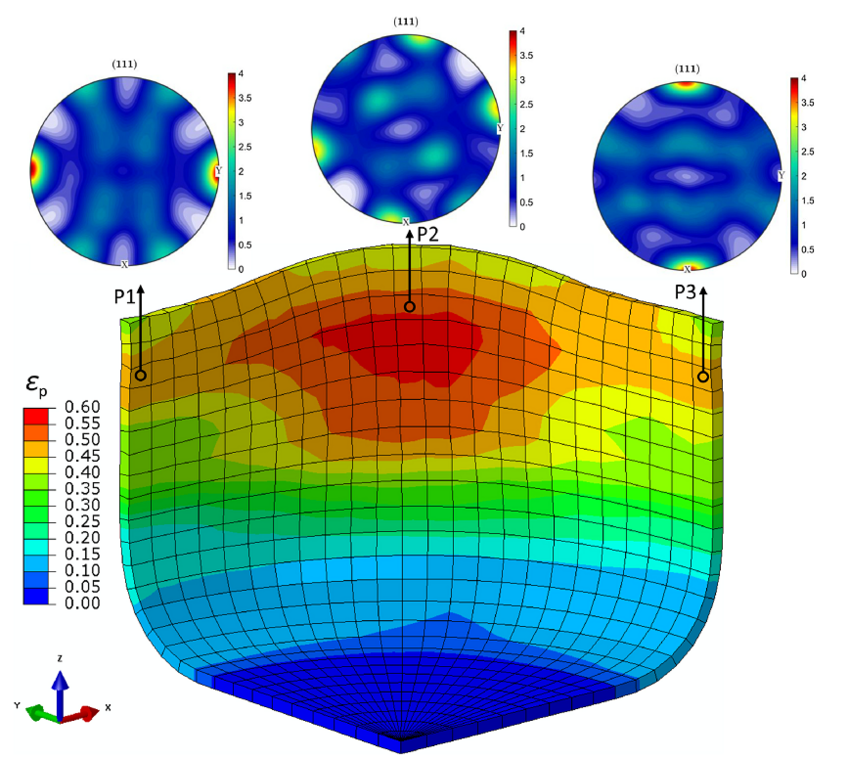
Deformed configuration and equivalent plastic strain (εp) distribution of the cup simulated with the evolving Yld2000-2D yield function starting from the central layer texture. The final textures at the three positions indicated are also shown.