Building an ab initio potentiostat
A fundamental challenge in modelling reactions at electrochemical solid-liquid interfaces is that they represent a thermodynamically open system: Conditions of constant electrode potential and pH are achieved by exchange of electrons and atoms (such as H) with the environment.
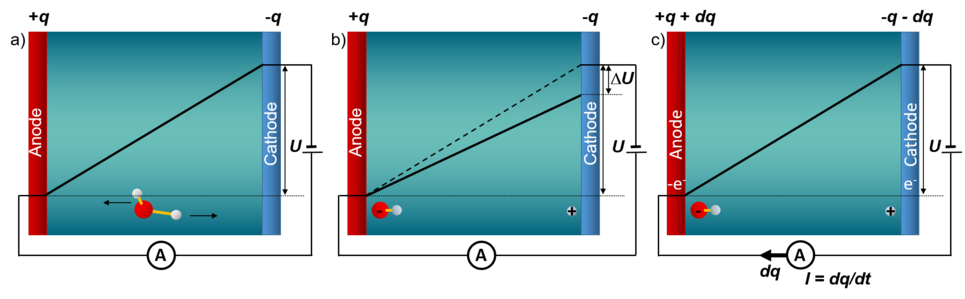
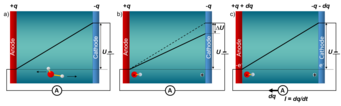
Experimentally, constant electrode potential conditions are realised by using a potentiostat. The shown schematic picture of an electrolytic cell illustrates the underlying principle: a positively charged electrode (anode) and a negatively charged electrode (cathode) are immersed in an aqueous environment. The electric field between the electrodes drives negatively charged ions (such as OH-) to the positively charged anode and positively charged ions (such as H+) to the cathode. The ensuing potential drop due to screening by the ions is counteracted by a potentiostat, which ensures that the constant electrode potential U is maintained, by transferring the amount of electrons needed to compensate the potential drop DU between the electrodes. Obviously, the single electrode within this setup is intrinsically grand-canonical, however, the full cell, which contains both the positively and the negatively charged electrode, is canonical for both electrons and protons.
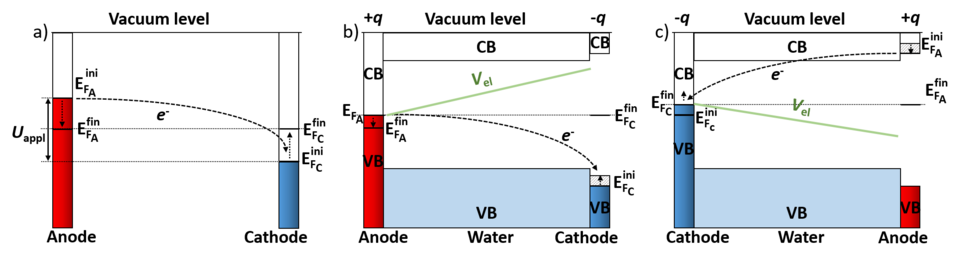
To realize such a canonical setup within a conventional density functional theory (DFT) code with periodic boundary conditions, if have to control the Fermi levels of the two electrodes, which is a prerequisite for a potentiostat. The difficulty lies within the mandatory condition for having a constant Fermi level throughout the cell in a standard DFT supercell calculation. To overcome this fundamental limitation we use a novel type of computational electrode by replacing one of the metallic electrodes (Fig. 2a) by a doped semiconductor (Fig. 2b and c). If the semiconductor is not doped and the Fermi level of the metal electrode falls within the bandgap of the semiconductor electrode, the two electrodes are decoupled and no charge transfer from one to the other electrode can occur. To transfer charge from one electrode to the other and build up a potential difference (potentiostat) between the two electrodes, we dope the semiconductor electrode n-type (to charge it positively and make it the anode) or p-type (to make it the cathode). The n-doped electrode (Fig. 2c) transfers its excess electrons from the conduction band to the metallic electrode, leaving the semiconductor electrode with a positive charge q and the metallic electrode with a charge -q. Due to Gauss law this charge transfer induces a potential bias U as well as an electric field. Controlling the doping charge q enables us to control the bias and field. A p-type doped electrode (Fig. 2b) changes the polarity of the field.
We identified Ne as the material most suitable to act as a computational semiconductor electrode: (i) it is the material with the largest band gap known in nature and suitably aligned to the water band gap, (ii) it is a Van der Waals bonded materials and has thus a negligible deformation potential and (iii) it is is chemically inert, so that chemisorption or alloy formation on this electrode is suppressed. We also find that even a single Ne layer prevents permeation of water molecules or of its residues such as H+ or OH-.
To dope the Ne electrode we utilize the concept of pseudo-atoms [1], which gives us the freedom to change the electrode charge by fractional numbers. To construct a Ne electrode consisting of nNe atoms with charge q we change the proton number of Ne from ZNe to ZNe+q/nNe. The number of valence electrons is also increased by q/nNe, so that the pseudo-atom is charge neutral. Since q/nNe is a small fraction of an electron the band structure (bandgap) of the Ne electrode remains almost unchanged except that it contains q excess electrons in the conduction or (for negative q values) q holes in the valence band. This construction gives us full control over the electrode charge and thus provides a central element to construct a static or dynamic potentiostat, i.e., with a constant or variable applied bias.
The setup of an electrolytic electrochemical cell employing standard DFT supercell calculations is straightforward: we fill the space between the metal and the Ne electrode by electrolyte (e.g. water) and add a vacuum region on the outside. To restore the overall periodic spatial variation of the potential, while having a potential U between the two electrodes, we include a dipole correction in the middle of the vacuum region [2]. The voltage obtained by the dipole correction is a direct measure of the electrode potential at the interface. The total dipole moment of the system, which is computed from the dipole correction, varies with the amount of charge transfer between the electrodes and reflects the extent to which the aqueous electrolyte screens the applied electric field. Consequently, controlling the total dipole moment during the course of the simulation controls the electrode potential of the interface, which allows us to adjust the charge supplied to the system to maintain a constant potential dynamically, in analogy to an experimental static potentiostat. We use pyiron [3] to set-up the feedback-loop and maintain a constant potential.
[1] K. Shiraishi, J. Phys. Soc. Jpn. 59, 3455 (1990).
[2] J. Neugebauer and M. Scheffler, Phys. Rev. B 46, 16067 (1992).
[3] J. Janssen, S. Surendralal, Y. Lysogorskiy, M.Todorova, T. Hickel, R. Drautz, J. Neugebauer, Comp. Mater. Sci. 163, 24 (2019)