Phase Stability and Short-Range Order of High Entropy Alloys
A high degree of configurational entropy is a key underlying assumption of many high entropy alloys (HEAs). However, for the vast majority of HEAs very little is known about the degree of short-range chemical order as well as potential decomposition. Recent studies for some prototypical face-centered cubic (fcc) HEAs such as CrCoNi showed that short-range order (SRO) can influence critical materials properties as, e.g., stacking fault energies. For refractory HEAs, due to slow diffusivity chemical ordering may hardly ever be achieved under typical experimental conditions but could potentially influence creep properties long-term applications. In this project we therefore study the phase stability and short-range order of selected fcc as well as bcc refractory HEAs computationally.
In principle, simulations at the atomic scale have complete access to short-range order (SRO) but encounter the challenge of accurately sampling high-dimensional configuration spaces. This is crucial for identifying the thermodynamic and kinetic conditions under which SRO is formed, as well as understanding its impact on material properties. With the advent of machine-learning potentials, such calculations have become feasible.
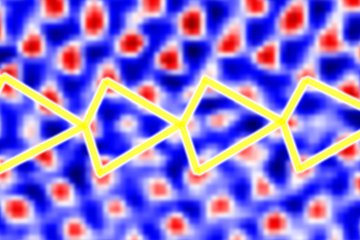
We utilize machine-learning methods, specifically the low-rank potential (LRP) method, in conjunction with explicit supercell calculations. This combined approach allows us to account for atomic relaxations in a manner similar to cluster expansion techniques, while also being computationally more efficient. One of our primary focuses is on body-centered cubic (bcc) refractory alloys, such as the bcc NbMoTaW high-entropy alloys (HEAs). Our research has demonstrated that, although local relaxations do not significantly affect short-range order parameters, they play a crucial role in understanding decomposition and phase stability at moderate temperatures. Furthermore, we have identified a new, intermediate relaxation-stabilized layered structure in this alloy.
Magnetism poses a fundamental challenge in computations related to phase stability. For the prototypical face-centered cubic (fcc) CrCoNi alloy, we have developed a framework to explore various magnetic scenarios, including the magnetic ground state and a paramagnetic condition. Significant magnetic energies have been observed in certain mixed L12/L10 ordered configurations, which are rooted in strong nearest-neighbor magnetic exchange interactions and chemical bonding among the constituent elements. We discovered a delicate interplay between magnetism and the stability of MoPt2 and L12/L10 ordering, which may help explain the conflicting findings reported in experimental and theoretical studies.
Further reading
Other related projects on HEAs are, e.g., on interstitial alloying.
Acknowledgments
This work was supported by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) within the special priority programme “Compositionally Complex Alloys – High Entropy Alloys (CCA-HEA)” (SPP 2006) and via Project number 429582718.