Big data and machine learning in electron microscopy
Data-rich experiments such as scanning transmission electron microscopy (STEM) provide large amounts of multi-dimensional raw data that encodes, via correlations or hierarchical patterns, much of the underlying materials physics. With modern instrumentation, data generation tends to be faster than human analysis, and the full information content is rarely extracted. We therefore work on automatizing these processes as well as on applying data-centric methods to unravel hidden patterns. At the same time, we aim at exploiting the insights from information extraction to direct the data acquisition to the most relevant aspects, and thereby avoid collecting huge amounts of redundant data.
The advent of fast electron detectors enabled the collection of full diffraction patterns in each probe-position, while scanning the beam across the electron transparent sample. These 4D-STEM datasets contain rich information on local lattice orientation, symmetry and strain [2]. However, handling and analysing these large-scale datasets, which are typically >10 GB in size requires sophisticated data management infrastructure and algorithms. We are currently developing a flexible and open-source approach within the Python-based pyXem package to index the phase and crystal orientation in scanning nano-beam diffraction datasets [3], which is until now only possible by commercial software. The development will also enable an on-the-fly data analysis in the future by utilizing GPU-accelerated processing.
STEM is also very powerful at revealing the atomic structure even of complex materials. Since under high-angle angular dark field (HAADF) conditions the collected electrons predominantly undergo scattering near the atomic nucleus, the image or atomic column intensity is proportional to their mean atomic number. When aligning the specimen along specific crystallographic directions it is possible to image a 2D projection of the crystal lattice, but also lattice defects such as phase or grain boundaries. Typically, the detection of nanoscale domains and interfaces in complex materials is executed by hand in an iterative manner relying on deep domain knowledge. We have developed a robust symmetry-based segmentation algorithm that solely considers lattice symmetries and hence does not require specific prior insights into the observed structures [4]. It is based on the idea that local symmetries create a self-similarity of the image that can be quantified via Pearson correlation coefficients of image patches. This quantification is very noise-tolerant, in particular if large patches are chosen. By collecting these values for a number of candidate symmetries (100-1000), a characteristic fingerprint of the local crystallographic patterns can be extracted that does not rely on identifying individual atomic columns. These fingerprints can then be taken from various places in the image and allow to filter out recurring patterns by principal component analysis and a subsequent clustering. From this abstract representation, the fingerprints can be classified, yielding a segmentation of the original image without prior training on expected phases. It therefore also works for complex atomic arrangements, e.g., topologically close-packed phases.
To classify and quantify regions autonomously in atomic resolution STEM images, we are currently developing a supervised deep learning approach in a BiGmax collaboration with L. M. Ghiringhelli (Fritz Haber Institute Berlin). The underlying backbone of the classification is a convolutional neural network (CNN), which is trained on simulated STEM images represented by their Fourier transforms. Here, we are considering the basic classes of face-centred cubic (fcc), body-centred cubic (bcc) and hexagonal close packed (hcp) crystal structure for low index orientations. To include uncertainty predictions in the classification, we use Bayesian learning for being able to identify crystal structures or defective regions that the CNN was not trained on. In a second step, the local crystal rotation and lattice parameters are determined by linear regression analysis, which is based on analysing the real space lattice symmetries. In the classification procedure, an experimental image is then subdivided in image patches and the neural network learns which training class is present, its local lattice rotation and lattice constants as shown in Fig. 1. This development is now extended towards a real-space classification procedure also taking into consideration the atomic column intensities to determine local compositional variations and defect structures.
![Fig. 1: Schematic workflow of the classification procedure for experimental STEM images. Here, the input HAADF-STEM image contains two different crystalline regions and one grain boundary. The image is divided into 5 × 5 windows. Three different patches are indicated in the input image: patch (1,1) by the blue, patch (3,3) orange and window (5,5) by the green square. The classification map identifies both blue and green patches as fcc {111}. The orange patches correspond to the grain boundary region, respectively [5]. Image by B.Yeo, L. Ghiringhell, Fritz Haber Institute Berlin.](/4691070/original-1643023773.jpg?t=eyJ3aWR0aCI6MTM3OCwib2JqX2lkIjo0NjkxMDcwfQ%3D%3D--66a31d25b3c258517c8e68f268752aa5f6d13b78)
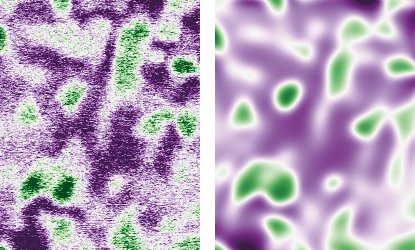
At larger length scales, HAADF allows to monitor phase transformations at elevated temperatures. Such time-resolved measurements yield multiple frames that can be visualized as video sequences. Yet, the quantification of the phase transformation kinetics requires additional processing and simplification of the raw data. In particular, the quantification of intensity gradients is severely hindered by the presence of shot noise. For this, we have explored the use of physics-informed neural networks to map the noisy images to a phase-field model with known analytic structure. The basic idea is to train a smooth machine-learning model to reproduce the measured data, while at the same time requiring it to comply with the phase-field equations, using model parameters that are trained on the fly. It turns out that such an approach is very efficient to obtain a coarse-grained simplified representation of the underlying data. In addition, the neural network representation and the phase-field equations filter out high-frequency noise in space and time without blurring interfaces (Fig. 2). These initial findings have triggered a new collaboration with the MPI for Dynamics of Complex Technical Systems, funded by the BiGmax network.
- https://nomad-coe.eu/home-coe
- Cautaerts, N.; Rauch, E. F.; Jeong, J.; Dehm, G.; Liebscher, C. H.: Scr. Mater. 201 (2021) 113930.
- Cautaerts, N.; Crout, P.; Ånes, H.W.; Prestat, E.; Jeong, J.; Dehm, G.; Liebscher, C.H.; in preparation.
- Wang, N.; Freysoldt, C.; Zhang, S.; Liebscher, C. H.; Neugebauer, J.: Microsc. Micronanal. (2021), in press.
- Yeo, B.C.; Leitherer A.; Scheffler M.; Liebscher, C.; Ghiringhelli, L.M.; in preparation
![Fig. 1: Schematic workflow of the classification procedure for experimental STEM images. Here, the input HAADF-STEM image contains two different crystalline regions and one grain boundary. The image is divided into 5 × 5 windows. Three different patches are indicated in the input image: patch (1,1) by the blue, patch (3,3) orange and window (5,5) by the green square. The classification map identifies both blue and green patches as fcc {111}. The orange patches correspond to the grain boundary region, respectively [5]. Image by B.Yeo, L. Ghiringhell, Fritz Haber Institute Berlin. Fig. 1: Schematic workflow of the classification procedure for experimental STEM images. Here, the input HAADF-STEM image contains two different crystalline regions and one grain boundary. The image is divided into 5 × 5 windows. Three different patches are indicated in the input image: patch (1,1) by the blue, patch (3,3) orange and window (5,5) by the green square. The classification map identifies both blue and green patches as fcc {111}. The orange patches correspond to the grain boundary region, respectively [5]. Image by B.Yeo, L. Ghiringhell, Fritz Haber Institute Berlin.](/4691070/original-1643023773.jpg?t=eyJ3aWR0aCI6ODQ4LCJmaWxlX2V4dGVuc2lvbiI6ImpwZyIsIm9ial9pZCI6NDY5MTA3MH0%3D--24e6141fc6a9e13547060f38d912aa64b67612ac)