Selectivity of solvent induced stabilisation of polar oxide surfaces
We study ZnO, which is of interest for applications ranging from catalysis, corrosion to opto- and micro-electronics, and focus on its (0001) surface as a prototypical example of a polar oxide surface. We combine density functional theory (DFT) calculations with a thermodynamic approach to construct surface Pourbaix diagrams, which reveal the stabile surface phases of the polar (0001) surface in dependence of the relevant conditions of the aqueous environment, characterized by the applied electrode potential U and the pH-value of the solution. To this end, we perform two types of DFT calculations for all considered surface reconstructions. In one set of DFT calculations, the surface is in contact with vacuum (a typical set-up, used to study surface science questions). In the second set of DFT calculations, the surface is in contact with an implicit solvent. To account for explicit chemical interactions of the solid surface with the aqueous environment, we include in the pool of possible surface reconstructions structures with adsorbed chemically reactive water constituents such OH- and H+ ions. The energetically much smaller effects due to hydrogen bonding between the solute and the solvent are not present in either set of calculations. Surface vibration entropy contributions, which are key to understanding the stabilization of ZnO(0001)-Zn surfaces in a gas phase environment [1], but we find to be small for temperatures relevant for wet electrochemistry (T ≈300 K), are not included.
The calculated DFT energies are used to evaluate the excess Gibbs free surface energy, ΔGα, of the investigated ZnO(0001)-Zn surface structures a:
ΔGα =( Eαtot − Ecleantot) −Σ Ni μi ,
referenced to the energies of the pristine surface Ecleantot and the reservoirs μi of elements i, of which Ni species are exchanged with the environment. Utilizing our grand-canonical approach extending methodologies widely used to study point defects in semiconductors [2, 3] to the description of stability and concentration of ions in liquids [4] we express the chemical potentials as a function of pH and electrode potential U. Hereby we use the relation
μH ( pH, U) = e(U – USHE) −kBT ln10 pH ,
in which USHE denotes the reference potential of the standard hydrogen electrode, and the conditions of thermodynamic stability for the involved phases, i.e.
μO =Δ fG [H 2O] −2μH and μZn = ΔfG[ZnO] –μO(μH).
![Fig.1: Surface Pourbaix diagrams for ZnO (0001)-Zn surfaces in aqueous environment. Colours are used to discriminate the different surface phases: structures with adsorbates on the smooth bulk terminated surface (blue), triangular reconstructions (red), adsorbate-passivated triangular reconstructions (green). The black hashed area shows the water stability region (see text). Inset are geometries (top view) of several of the stable surface reconstructions (O:red, Zn:gray, H: blue). The yellow star marks the experimental condition at which triangular reconstructions have been observed at the surface in an in situ AFMstudy (Inset) [5].](/3743688/original-1553503924.jpg?t=eyJ3aWR0aCI6OTY2LCJvYmpfaWQiOjM3NDM2ODh9--990eb62f4650e5efcbb50c1c5b2d3e13ac78f2a6)
study (Inset) [5].
The ensuing surface Pourbaix diagrams constructed using the DFT data without solvent (Fig.1 (left)) and with solvent (Fig.1(right)) are shown to the right provide direct insight into the selectivity of the solvent. For a solvent, which shows no selectivity, the two surface Pourbaix diagrams would have been identical. This is obviously not the case. In fact, the impact of the solvent is dramatic: It leads not only to a shift of the phase boundaries (which would indicate that one surface profits energetically more than the other does), but also to the stabilization of surface reconstructions that are thermodynamically unstable in an ambient gas phase environment. The left diagram, in which the effect of solvation is reduced to the chemisorption of the dissociated water fragments H and OH, is dominated by structures with adsorbates on the bulk terminated surface (blue colours). The right diagram is dominated by triangular reconstructions (red and green colours). We note, that only the right diagram, constructed from DFT energy calculations with explicitly included solvation effects, is able to account for the experimental observation of triangular phases, as seen in in situ AFM experiments by Valtiner et al. [5] at open circuit potential conditions (U – USHE = 0V) and pH ≈ 3 (marked by a yellow star).
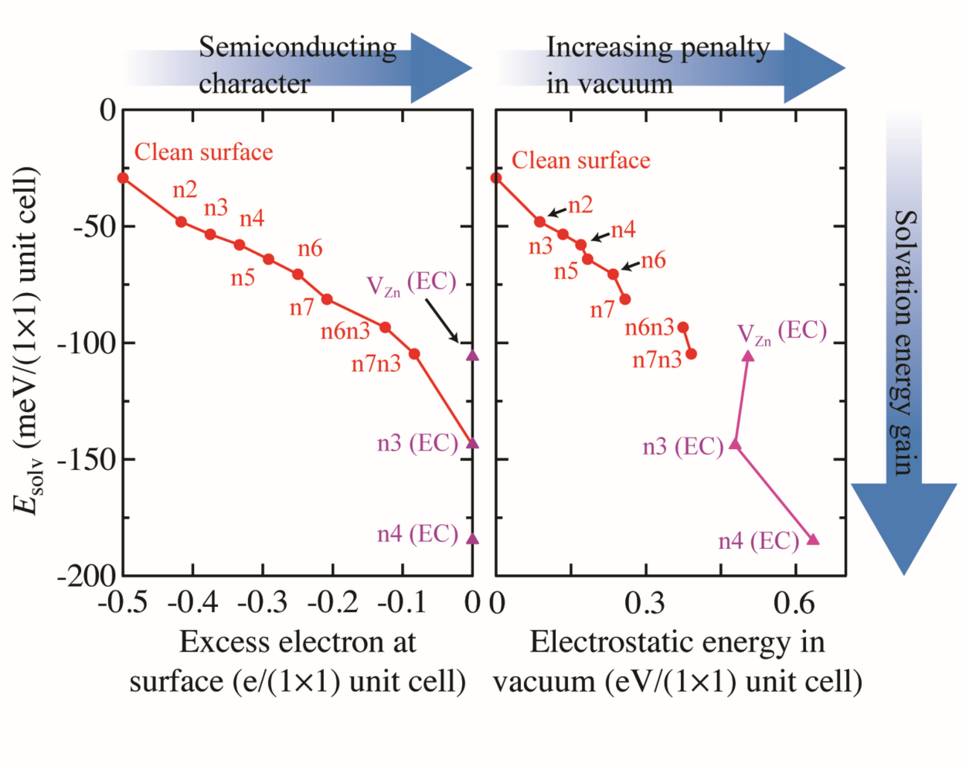
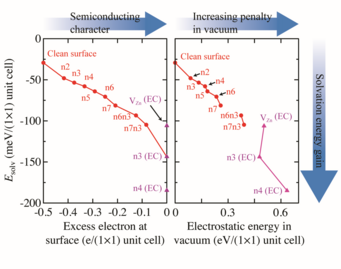
To understand why triangular reconstructions are so strongly favoured by the electrolyte compared to the other considered surface reconstructions we evaluate the solvation energy, Esolv. The solvation energy, which is the energy difference between the DFT total energy of the system in vacuum and the system in contact with the solvent, shows a dependence on both the amount of unpaired electrons at the surface (Fig. 2 (left)), as well as on the surfaces’ electrostatic energy (Fig.2(right)). Because the amount of unpaired electrons at the surface is a measure of the surface’s metallicity and its deviation from charge neutrality, the decrease in solvation energy with increasing metallicity, reveals that solvation strongly favours non-metallic surfaces over the ones with metallic character. The strong selectivity towards non-metallic surface structures is a consequence of the screening propensity of the respective surfaces. Metallic surfaces, which have a much higher intrinsic electronic polarizability, can screen electrostatic charges much more efficiently compared to semiconducting surfaces. Consequently, the solvent provides an almost metallic screening (the dielectric constant of water is 80) to surfaces, which are semiconducting, reducing electrostatic penalties at the surface. For surfaces with metallic character (i.e. surfaces with an excess of electrons or holes), where screening is already an intrinsic part of the surface, additional screening by the solvent brings no additional energy gain. Furthermore, surfaces experiencing a higher electrostatic penalty in vacuum naturally gain more energy by screening. Thus, triangular reconstructions, which are unfavourable from an electrostatic point of view in vacuum, due to the large separation between negative charges at the triangle edges (filled O dangling bonds) and positive charges inside the triangle (empty Zn dangling bonds), will gain a higher solvation energy compared to the non-triangular structures.
The correlations identified in this study reveal that the solvation effects are substantial, highly discriminating and key to understand and eventually control the appearance and thermodynamic stability of structures at semiconducting surfaces.
[1] M. Valtiner, M. Todorova, G. Grundmeier, and J. Neugebauer, Temperature Stabilized Surface Reconstructions at Polar ZnO(0001), Phys. Rev. Lett. 103, 065502 (2009).
[2] C. G. Van de Walle and J. Neugebauer, First-principles calculations for defects and impurities: Applications to III-nitrides, J. Appl. Phys. 95, 3851 (2004).
[3] C. Freysoldt, B. Grabowski, T. Hickel, J. Neugebauer, G. Kresse, A. Janotti, and C. G. Van de Walle, First-principles calculations for point defects in solids, Rev. Mod. Phys. 86, 253 (2014).
[4] M. Todorova and J. Neugebauer, Extending the concept of defect chemistry from semiconductor physics to electrochemistry, Phys. Rev. Applied 1, 014001 (2014).
[5] M. Valtiner, S. Borodin, and G. Grundmeier, Langmuir 24, 5350 (2008).
![Fig.1: Surface Pourbaix diagrams for ZnO (0001)-Zn surfaces in aqueous environment. Colours are used to discriminate the different surface phases: structures with adsorbates on the smooth bulk terminated surface (blue), triangular reconstructions (red), adsorbate-passivated triangular reconstructions (green). The black hashed area shows the water stability region (see text). Inset are geometries (top view) of several of the stable surface reconstructions (O:red, Zn:gray, H: blue). The yellow star marks the experimental condition at which triangular reconstructions have been observed at the surface in an in situ AFMstudy (Inset) [5]. Fig.1: Surface Pourbaix diagrams for ZnO (0001)-Zn surfaces in aqueous environment. Colours are used to discriminate the different surface phases: structures with adsorbates on the smooth bulk terminated surface (blue), triangular reconstructions (red), adsorbate-passivated triangular reconstructions (green). The black hashed area shows the water stability region (see text). Inset are geometries (top view) of several of the stable surface reconstructions (O:red, Zn:gray, H: blue). The yellow star marks the experimental condition at which triangular reconstructions have been observed at the surface in an in situ AFMstudy (Inset) [5].](/3743688/original-1553503924.jpg?t=eyJ3aWR0aCI6MzQxLCJmaWxlX2V4dGVuc2lvbiI6ImpwZyIsIm9ial9pZCI6Mzc0MzY4OH0%3D--a627d5a7d82f4b7afbfdbc6be188da8dcb4c282d)