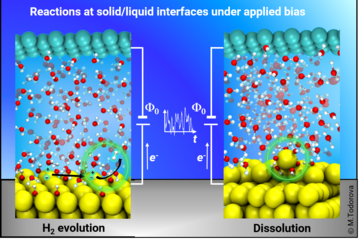
Stability of polar ZnO(0001) surfaces in dry and humid environment
ZnO is a wide band gap semiconductor which is of interest to such diverse areas of application as passivation layers on steel surfaces, catalysis, corrosion, adhesion, gas sensing, and micro- or optoelectronics. Understanding the surface structure and stoichiometry is of high practical interest and essential for any of the mentioned applications. Keeping in mind that the chemical environment interfacing with the surface plays a decisive role in the stabilisation and atomic structure of the surface reconstruction, we combine density functional theory (DFT) calculations with atomistic thermodynamics to investigate and understand the stability of polar Zn-terminated ZnO(0001) surfaces in dry and humid environment.
Temperature stabilised surface reconstructions
Based on energies Eσtot computed by DFT (σ denominates the corresponding surface reconstruction) we evaluate the excess Gibbs energy
ΔGσ[T, μα(pα,T)] = Eσtot - TΔSvib - ΣαNαμα
esulting from a reaction of the surface with atoms in the surrounding (ambient) gas phase. Here Nα is the number of surface atoms of species α with corresponding chemical potential μα and T is the temperature at and near the surface.
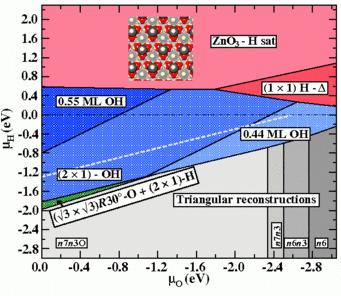
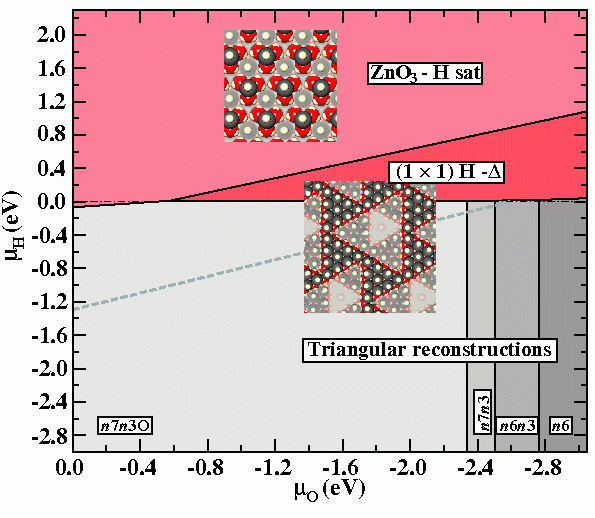
![Fig.1: Surface Pourbaix diagrams for ZnO (0001)-Zn surfaces in aqueous environment. Colours are used to discriminate the different surface phases: structures with adsorbates on the smooth bulk terminated surface (blue), triangular reconstructions (red), adsorbate-passivated triangular reconstructions (green). The black hashed area shows the water stability region (see text). Inset are geometries (top view) of several of the stable surface reconstructions (O:red, Zn:gray, H: blue). The yellow star marks the experimental condition at which triangular reconstructions have been observed at the surface in an in situ AFMstudy (Inset) [5].](/3743688/original-1553503924.jpg?t=eyJ3aWR0aCI6OTY2LCJvYmpfaWQiOjM3NDM2ODh9--990eb62f4650e5efcbb50c1c5b2d3e13ac78f2a6)
study (Inset) [5].
In contrast to observations for other materials and common belief we find that the vibrational entropy of ZnO surface atoms, ΔSvib, has an unexpectedly large impact on the stabilisation of surface geometries. This is a consequence of a variety of surface structures with similar stoichiometry, but very different geometry lying energetically in close proximity to each other.
The resulting explicit temperature dependence of the excess energy ΔGσ[T, μα(pα,T)] requires the construction of temperature dependent surface phase diagrams. Such diagrams are shown to the right (Fig.1) for a ZnO(0001)-Zn surface in contact with a humid oxygen environment. The upper diagram depicts the T = 0 K situations, which can also be identified with the case commonly observed for other materials, in which the excess surface energy ΔGσ[μα(pα,T)] is only implicitly temperature dependent via the chemical potential of the gas phase. Inlayed are geometries of the stable structures.
The lower surface phase diagram in Fig.1 corresponds to T = 950°C. The change in the phase boundaries at T = 450°C for two of the observed structures are marked by dot filled regions curtailed by dashed lines. The morphologies of these two structures are shown in between the phase diagrams for T = 0K and T > 0K and are a (2×2)-O adsorbate structure and a (√3×√3)R30°-O backbone structure with H atoms adsorbed on-top of the O atoms in a (2×1) arrangement.
This presentation of the temperature driven changes within the T > 0 K diagram enables us to make direct comparison to experimental observations. For samples annealed in dry oxygen atmosphere (p (O2) = 1 bar, p (H2O) = 0.2 mbar) the only phase observed even after cool down from 1223K to 723K is the (2×2)-O structure (path (A) in the diagram). For samples annealed in humid oxygen atmosphere (p (O2) = 0.96 bar, p (H2O) = 40 mbar) a phase transition from the (2×2)-O to the (√3×√3)R30°-O+(2×1)H structure is observed upon cool down from 1223K to 723K (path (B) in the diagram). The computed phase diagram allowed to consistently explain the occurrence of hitherto controversially discussed surface structures and accounts nicely for the experimental observations.
Hydrogen adsoption and kinetically stabilised structures
Considering that thermodynamic equilibrium cannot be always reached under realistic conditions the conventional thermodynamic approach that is based on the assumption of full thermodynamic equilibration seems to have only limited applicability. On the other hand, assuming equilibrium conditions is highly appealing as it requires only consideration of initial and final state. We extended this approach to the computation of meta-stable diagrams, which enabled us to understand one of the most puzzling structures found on polar ZnO(0001)-Zn surfaces – a so-called (1×1) hydrogen structure.
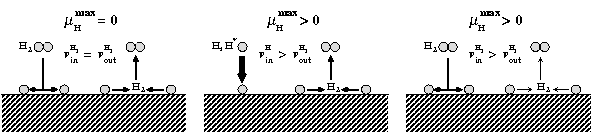
The route to extending surface phase diagrams to include kinetically stabilized surface reconstructions can be understood by considering the schematic figure below:
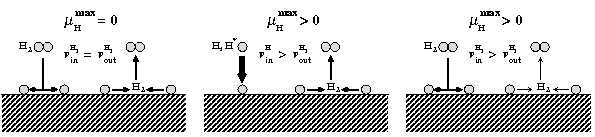
Assuming thermodynamic equilibrium between a surface and a surrounding, e.g., H gas phase means that the maximal chemical potential an H atom at the surface can possess is equal to the one of an H2 molecule in the gas phase (left panel). To realise such equilibrium a sufficiently fast exchange between H atoms at the surface and in the gas phase must be possible. Furthermore, the exchange cannot be realised by desorbing H atoms, since the reference is an H2 molecule in the gas phase. This means, that before desorption any two H atoms have to recombine at the surface forming a weakly bound H2 molecule that can easily desorb. If the H exchange between surface and gas phase is kinetically hindered, hydrogen chemical potentials beyond the thermodynamic limit (μ(H2) = 0) will be realised. This will be, e.g., the case if the adsorption channel (incoming H flux) exceeds the recombination channel (middle panel) or should the recombination process be highly activated (right panel).
Under realistic experimental conditions H may occur in the form of molecules, which are meta-stable with respect to H2 formation, in the form of a H plasma, in which the molecules are electronically excited or even in the from of H atoms. Each of these situations will lead to the realisation of hydrogen chemical potentials higher than the one of the H2 molecule.
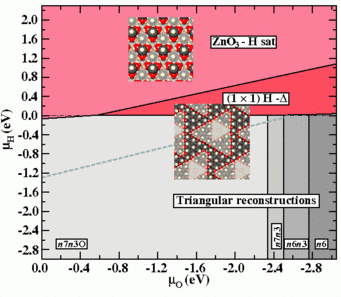
Following these consideration, we extend the phase diagram to regions above the chemical potential of the H2 molecule, which leads to an inclusion of kinetically stabilised surface reconstructions into it. By shifting the upper limit of the H-chemical potential in the diagram, regions which are thermodynamically unstable against the formation of H2, but thermodynamically meta-stable in the absence of H2 formation become accessible.
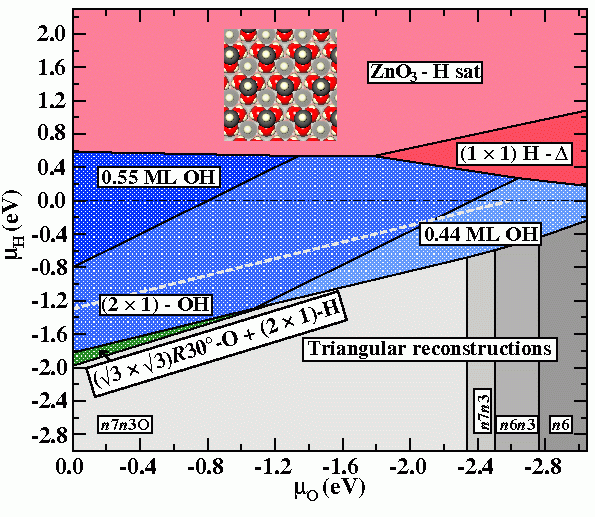
When one considers possible adsorbate structures stabilising a polar ZnO surface, a (1×1)-H adsorbate structure is counterintuitive, since it is not conform to the electron counting rule, which results in local charge neutrality. (This rule [1] requires, that all available electrons in the surface layer are distributed such, that the dangling bonds of the electro-negative element (O) are filled, leaving the dangling bond states of the electro-positive element (Zn) empty.) However, Wöll and co-workers have observed a structure with (1×1) symmetry following H-exposure by He-scattering thermal desorption experiments (TDS) [2]. This experiments further suggest that the structure is only meta-stable, while XPS data show the presence of both Zn-H and O-H species at the surface.
Within the extended region of the shown phase diagram the structure coined “(1×1)H-Δ” would appear as a (1×1)-H structure in He-TDS experiments, event though it does not comprise a (1×1) structure in the strict crystallographic sense. It consist of a n7n3O-triangular reconstruction found within the stable region of the phase diagram, which is covered entirely by H atoms, i.e. both surface Zn atoms and edge O atoms are protonated.
Finally we note that the experimental observation of meta-stable structures may be also the consequence of the inability of the thermodynamically stable surface to form, due to the requirement of massive rearrangements of atoms at the surface. In such a case, thermodynamic equilibrium may be a slow process and hard or even impossible to achieve. To account for this kinetic limitations the thermodynamic phase diagram has to be replace by a meta-stable phase diagram, from which thermodynamically stable but kinetically forbidden structures have been removed (Fig.4).
The surface pre-treatment by cycles of sputtering and annealing employed by Wöll and co-workers, preceding the H exposure, result in a surface stabilised by triangular reconstructions. Given the massive reconstructions needed to realise hydroxyl ad-atom structures (phases removed from the last diagram), establishing thermodynamic equilibrium seems very unlikely. Consequently observation of triangular reconstructions beyond their region of thermodynamic equilibrium may be expected.
[1] W.A. Harrison, Electronic Structure and Properties of Solids, Dover Publications, Inc., New York, 1989; M.D. Pashley, Phys. Rev. B 40, 10481 (1989).
[2] T. Becker et al., Surf. Sci. 486, L502 (2001); Ch. Wöll, J. Phys.: Condens. Matter 16, S2981 (2004).
![Fig.1: Surface Pourbaix diagrams for ZnO (0001)-Zn surfaces in aqueous environment. Colours are used to discriminate the different surface phases: structures with adsorbates on the smooth bulk terminated surface (blue), triangular reconstructions (red), adsorbate-passivated triangular reconstructions (green). The black hashed area shows the water stability region (see text). Inset are geometries (top view) of several of the stable surface reconstructions (O:red, Zn:gray, H: blue). The yellow star marks the experimental condition at which triangular reconstructions have been observed at the surface in an in situ AFMstudy (Inset) [5]. Fig.1: Surface Pourbaix diagrams for ZnO (0001)-Zn surfaces in aqueous environment. Colours are used to discriminate the different surface phases: structures with adsorbates on the smooth bulk terminated surface (blue), triangular reconstructions (red), adsorbate-passivated triangular reconstructions (green). The black hashed area shows the water stability region (see text). Inset are geometries (top view) of several of the stable surface reconstructions (O:red, Zn:gray, H: blue). The yellow star marks the experimental condition at which triangular reconstructions have been observed at the surface in an in situ AFMstudy (Inset) [5].](/3743688/original-1553503924.jpg?t=eyJ3aWR0aCI6MzQxLCJmaWxlX2V4dGVuc2lvbiI6ImpwZyIsIm9ial9pZCI6Mzc0MzY4OH0%3D--a627d5a7d82f4b7afbfdbc6be188da8dcb4c282d)