A multiscale Study of the H enhanced Local Plasticity Mechanism
Local hydride formation around dislocations induces stress-shielding effects and is the underlying mechanism for hydrogen-enhanced local plasticity (HELP). To understand the phenomenon, a hierarchal multiscale approach is employed, combining ab-intio simulations, semi-empirical atomistic potentials and analytic models. The strategy involves passing information gained from ab initio and atomistic calculations to inform analytic models that predict macroscopic phenomena that are observable in experiments.
Introduction: Mechanisms of hydrogen embrittlement in metals
Hydrogen embrittlement can be loosely defined as a structural deterioration of materials under the influence of hydrogen. The effect has been observed in fcc, bcc and hcp materials and is particularly pronounced in high strength steels. The mechanisms underlying the observed embrittlement are still not fully understood, despite extensive research efforts in the field for over a century [1].
The proposed mechanism broadly falls into one of three categories: stress-induced hydride formation, hydrogen induced decohesion (HEDE) and hydrogen enhanced local plasticity (HELP). Stress-induced hydride formation is relatively well-established for hydride forming metals. Nucleation and growth of the hydride phase in the presence of stress concentrations enable the brittle fracture mode in these materials. In the HEDE mechanism, the hydrogen atoms accumulate within the lattice and reduce the cohesive energy of the metal matrix. This lowers the energy required to cleave the crystal along certain crystallographic planes, grain boundaries or phase boundaries.
The distinctly plastic nature of the fracture surface in a whole range of metals led to the development of the HELP mechanism. It is based on the assertion that the mobility and formation energy of dislocations is reduced in regions of high hydrogen content, such as notches or crack tips. The corresponding increase in plasticity is therefore localized to these regions, resulting in slip localization, constrained plasticity and finally localized plastic fracture.
Stress shielding and modulus effect
On an atomistic level the HELP mechanism is based on the so-called stress shielding and modulus effects. The H induced stress shielding effect results in increased dislocation mobility by shielding the repulsive stress-mediated interaction between dislocations. The modulus effect, on the other hand, describes a reduction in the shear modulus, as well as in the stacking fault energy of metals in the presence of hydrogen, which results in a reduction in the Peierl’s and dislocation nucleation barrier.
The stress shielding effect is supported by experimental evidence based on in-situ TEM studies, which revealed increased dislocation velocities in the presence of hydrogen, as well as reduced dislocation-dislocation separations in dislocation pile-ups at dislocation barriers, such as grain boundaries. These experimental observations led to the development of a semi-quantitative model based on continuum mechanics simulations that predicted significantly reduced dislocation-dislocation interactions in the presence of hydrogen. The model treats the H-dislocation interaction using a mean field approach solely based on the elastic interaction between the dilatational stain field of interstitial H atoms and the stress field of the dislocation, while H-H interactions, which have been shown to significantly affect H distributions around dislocations [2], are disregarded.
Aims
The aim of the current study is to quantify hydrogen-hydrogen interaction in metals and incorporate them in determining the equilibrium concentration of hydrogen around dislocations. NiH was used as a model system, as H-induced, locally plastic fracture has been observed in Ni [3] and well-established semi-empirical (EAM) interaction potentials [4,5] are available for this system.
A multiscale approach for a scale-transcending problem
The stress-shielding mechanism is challenging to model on an atomistic level, as it involves interactions at various length scales, which necessitates a multi-scale approach. On one hand, accurately determining metal-hydrogen and hydrogen-hydrogen interactions requires, in principle, an ab initio electronic structure calculation. On the other hand, the hydrogen-dislocation interaction depends on the dislocation's long range stress field (~1/r) and necessitates system sizes on the order of thousands of atoms. Additionally, finite temperature effects play an important role in determining the hydrogen concentration around the dislocation. Unfortunately, directly simulating these systems at finite temperature is not practical due to the time-scales associated with the relevant deformation mechanisms.
In order to incorporate all these elements, a hierarchical multiscale approach is adopted. In this approach, Density Functional Theory (DFT) and semi-empirical embedded atom method (EAM) calculations are used to develop an chemically and atomistically informed analytic model.
Results
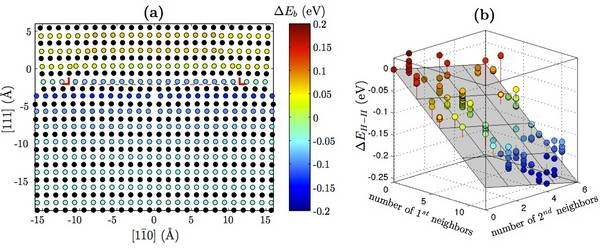
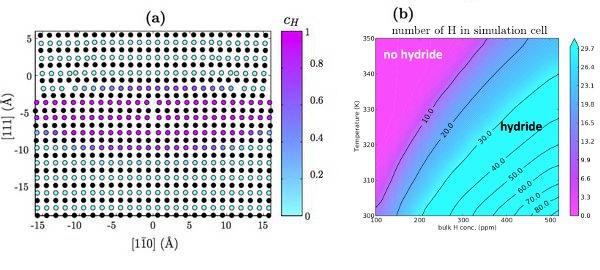
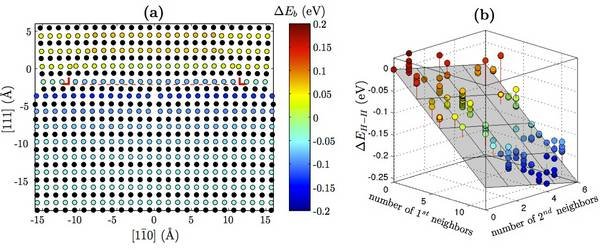
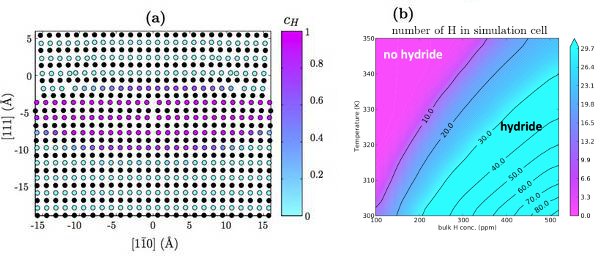
DFT calculations are used to validate a modified EAM potential for nickel-hydrogen systems. Using this potential, the hydrogen-dislocation interaction (Fig. 1a) is determined as a function of hydrogen position. Additionally, hydrogen-hydrogen interaction (Fig. 1b) is determined as a function of nearest neighbors. These serve as input to an analytic model that calculates the equilibrium concentration of hydrogen around the dislocation as a function of temperature and bulk hydrogen concentration (Fig. 2a). The results are consistent with previous Monte Carlo calculations [6]. By taking advantage of the computational efficiency of the analytic model, the onset of the HELP mechanism is predicted (Fig. 2b).
References
[1] W. H. Johnson, Proc. R. Soc. 23, 168 (1875).
[2] I. M. Maxelon, A. Pundt. W. Pyckhout-Hintzen, J. Barker and R. Kirchheim, Acta Mater. 49, 2625 (2001).
[3] I. M. Robertson and H. K. Birnbaum, Acta Metall. 34, 353 (1986).
[4] J. E. Angelo, N. R. Moody and M. I. Baskes, Model. Simul. Mater. Sci. Eng. 3, 289 (1995).
[5] M. I. Baskes, X. Sha, J. E. Angelo and N. R. Moody, Model. Simul. Mater. Sci. Eng. 5, 651 (1997).
[6] J. von Pezold, L. Lymperakis, J. Neugebeauer. Acta Mat. 59, 2969 (2011).