Framework for Multi-Phase Material Modeling using Stabilized Interface and Crystal Plasticity Finite Element Methods
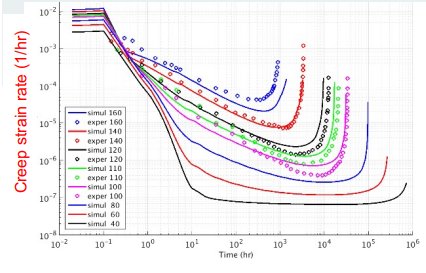
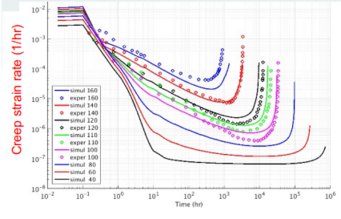
As computational resources have continued to expand, the drive for developing computational methods with higher fidelity for complex material modeling problems has continued to increase. A persistent challenge in computational multi-phase modeling is the robust treatment of non-smooth features or interfaces, such as grain boundaries in metals, interphases between constituents in composite materials, lubricated and bolted joints in structural systems, etc. Across these diverse applications, the major bottleneck revolves around imposing kinematic conditions upon discontinuous discrete functions in a mathematically consistent fashion. This talk explores our group’s efforts on deriving and advancing a stable computational framework for modeling solid mechanics problems with a range of interface kinematics. The framework serves as a robust platform for predictive modeling of mechanical and material systems containing interfaces due to the underlying philosophy of the variational multiscale method; two applications are the frictional dissipation in bolted mechanical joints and the debonding of fibrous composites. Also, our computational efforts have born fruit through collaborations with materials characterization groups to elucidate material mechanisms through physics-based crystal plasticity modeling. One area of interest is the creep behavior of Grade 91 ferritic/martensitic steel, particularly to extrapolate behavior from short-life/high-stress experiments to operating regimes.