A microscopic view of electrochemical interfaces: ab initio molecular dynamics at controlled electrode potential
Ever since the discovery of electricity, chemical reactions occurring at the interface between a solid electrode and an aqueous solution have aroused great scientific interest, not least by the opportunity to influence and control the reactions by applying a voltage across the interface. Our current textbook knowledge is mostly based on mesoscopic concepts, i.e. effective models with empirical parameters, or focuses on individual reactions decoupled from the environment, presenting therefore a serious obstacle for predicting what happens at a particular interface under particular conditions.
In particular the current transition of the world to a more sustainable future requires a truly microscopic understanding of the electrochemical interface and double-layer by incorporating insights from the atomistic and electronic scale. Methodological breakthroughs at the MPIE during the last few years in both ab initio theory and experiments now allow us to directly characterise the structure and dynamics of electrified solid/liquid interfaces with atomic resolution at short timescales.
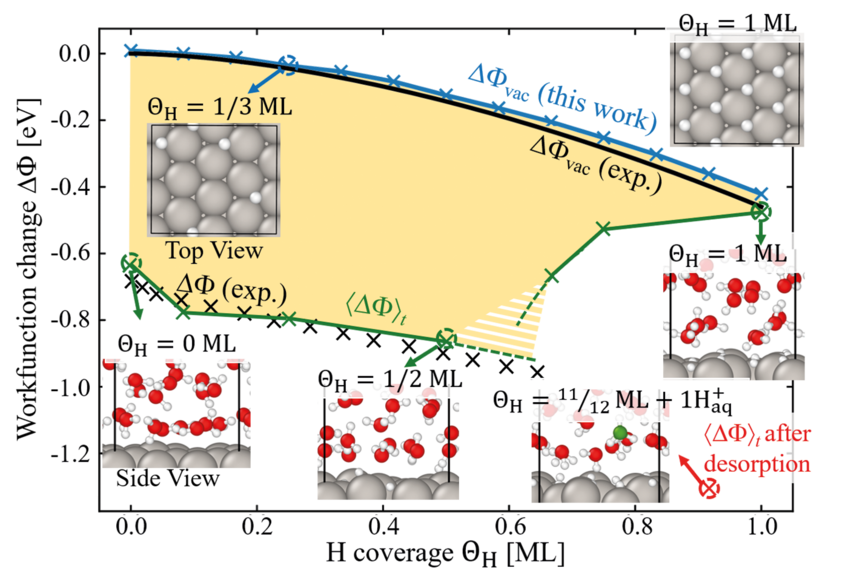
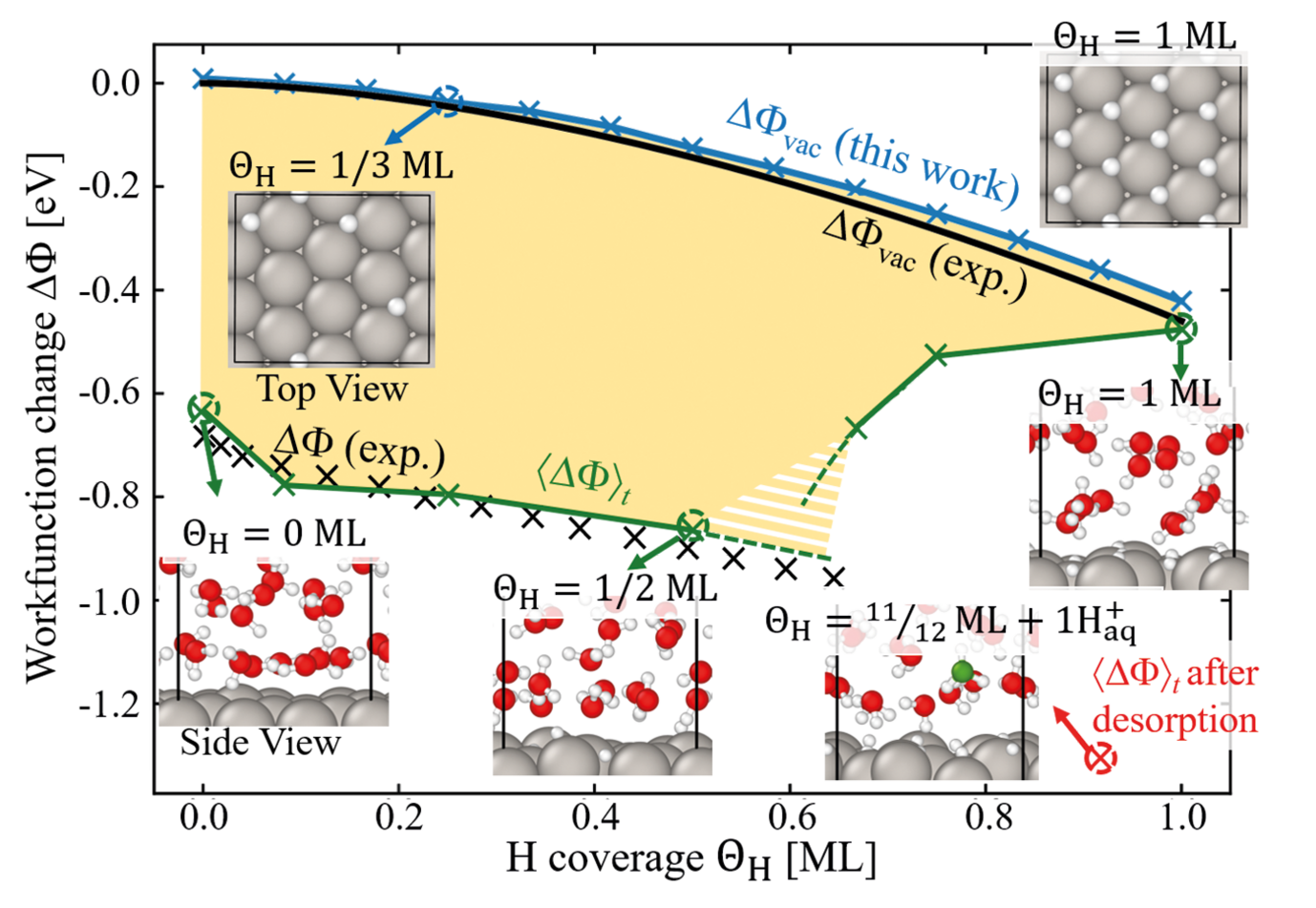
While the relation between the electrode potential and adsorbate coverage is accessible by experimental techniques such as cyclic voltammetry, understanding how exactly adsorbate interfacial structures influence the measured electrode potential evades direct experimental access. Consider the H-covered Pt(111)/H2O interface, one of the best investigated “model” electrochemical systems due to its excellent catalytic performance for the hydrogen evolution reaction (HER). The onset of the HER coincides with the presence of a puzzling upper limit to the H adsorption at ≈ 0.66 ML (monolayer). A possible explanation is that water is not just a spectator but actively controls adsorption and chemical reactions at the metal-water interface.
To explore the impact of water on surface adsorption and the electrode potential, we perform a systematic comparison of the work function (electrode potential) of H-covered Pt(111) in vacuum (an aqueous environment) for coverages up to 1 monolayer employing density functional theory calculations [1]. Our calculations show an excellent agreement with experiment (cf. Fig. 1) and allow us to directly explore how screening is realised at electrochemical interfaces. For the pristine Pt(111) interface we observe a large shift of the electrode potential with respect to the vacuum work function. This shift is caused by chemisorbed water molecules, which screen the interfacial dipole through charge transfer to the surface. Besides the Pt atom directly bonded to the H2O molecule, this transfer involves several Pt atoms in its vicinity, effectively blocking neighbouring adsorption sites. Therefore, with the onset of H adsorption a competition arises between the water and hydrogen for the Pt atoms available for charge transfer. Increasing H coverage causes a monotonous loss of chemisorbed water, which is partially compensated by the charge transfer, due to H adsorption, but causes an increasing potential drop. Beyond a critical coverage of qH » 0.66 ML this mechanism breaks down, because the increasing potential drop at the interface can no longer be screened by direct adsorption. Instead, the system responds by creating a large interfacial dipole through an electrochemical desorption reaction. This is achieved by deprotonation, where an H+ ion forms in the vicinity of the interface, leaving its corresponding electron at the Pt(111) surface. The H+ ion formation provides the necessary precursor state to enable the HER. Our findings directly link the existence of the breakdown in the electrode potential and the experimentally observed critical H adsorbate concentration at which hydrogen evolution starts.
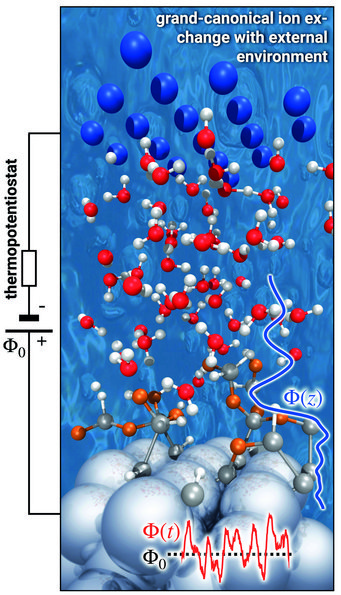
In order to study electrochemical reactions -- such as, e.g., the HER -- in ab initio molecular dynamics simulations with explicit water, we build on our first principles electrochemical cell set-up introduced in the last reporting period [2], which allows us to actively control the local surface charge in order to drive the system towards the targeted value for the electrode potential. While the surface charge is constant in the thermodynamic limit, the microscopic size of the interfacial region targeted by our simulations requires treating the local surface charge as a thermodynamic degree of freedom.
Changing the potential of a capacitive system, e.g. by controlling the surface charge in our electrochemical cell, is, however, a dissipative process. Energy is drained from molecular motions that are associated with a change in the electric dipole moment. This energy lost to potential control has to be compensated by corresponding thermal potential fluctuations, that exactly return the removed energy, on average, to those degrees of freedom where it was taken from. The physical system realises this by coupling to a fluctuating electric field created by temperature dependent charge fluctuations caused by the thermal motion of the electrons and ions.
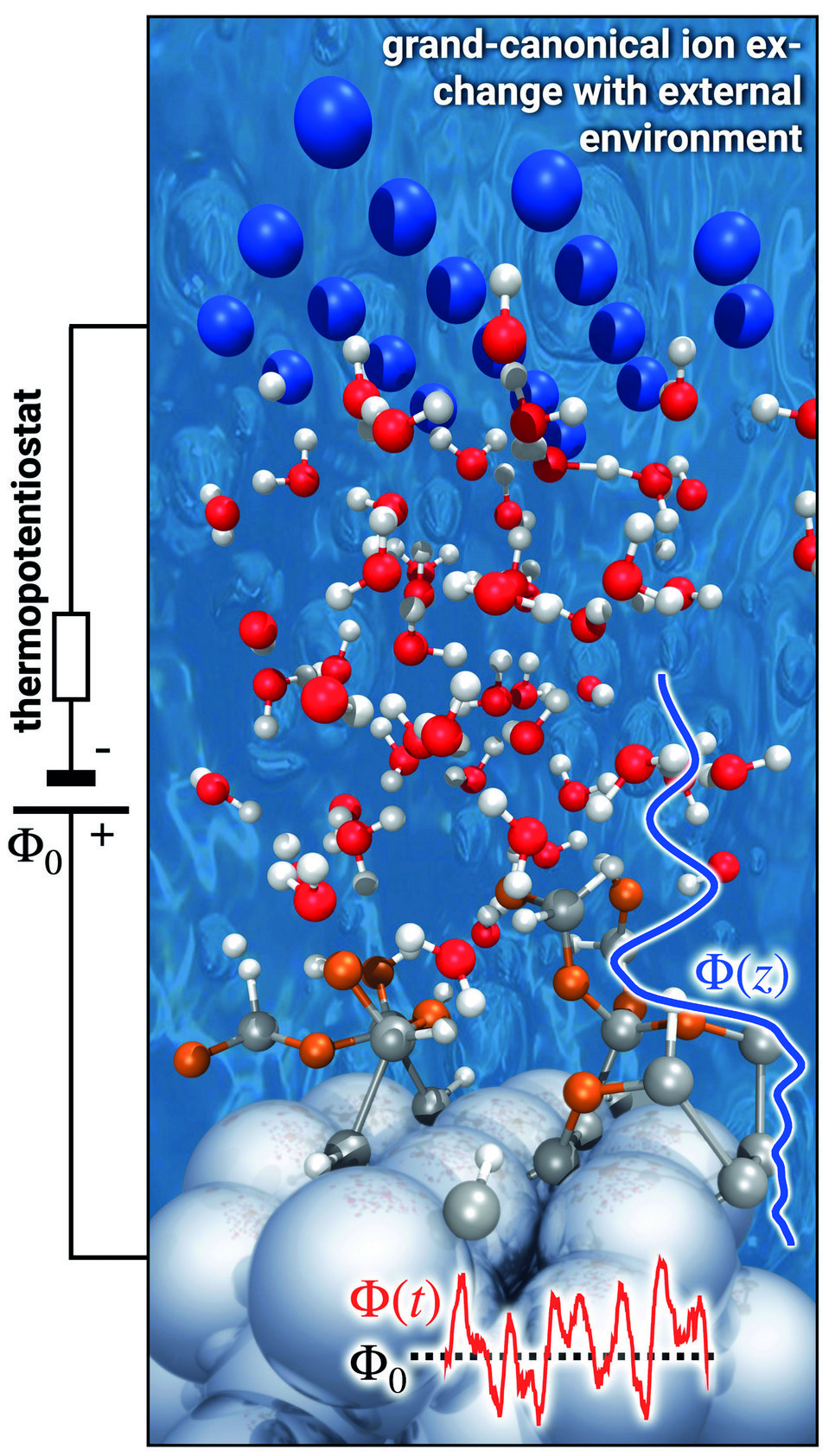
To mimic this behaviour, our potentiostat must apply an electric field with an explicit finite temperature and hence become a thermopotentiostat. This can be achieved by adapting the fluctuation-dissipation theorem (FDT) to atoms exposed to an electric field. To this end, we used the FDT and the theory of stochastic differential equations in conjunction with Itō calculus. The derived direct expression for the electrode charge [2] is general, independent of the specific boundary conditions of the set-up and can be straightforwardly implemented in any molecular dynamics code, whether empirical or first principles. In fact, we have already implemented the thermopotentiostat in the VASP and lammps simulation packages (Fig. 2).
To demonstrate the performance of our thermopotentiostat approach we considered a topic that currently attracts a lot of attention. Recent experiments demonstrated that the presence of a solid-water interface appears to dramatically reduce the dielectric response of water from a highly polarizable medium down to a response that is close to the vacuum dielectric constant. We found that interfacial water forms stratified structures with a strongly modified dielectric behaviour, showing characteristic oscillations in the dielectric function close to interfaces and overscreening effects reminiscent of Friedel oscillations. As a consequence of the interfacial water’s dielectric response, the potential drop between the electrode and the bulk water region occurs to a large degree directly at the interface, cf. blue line in Fig. 2. It is exactly within this region of interfacial water with modified properties where electrochemical reactions proceed.
Pioneered by Gerischer already 60 years ago, single-crystalline and atomically flat semiconductor surfaces interfaced with liquid water were popular model systems used to explore elementary electrochemical processes. The reaction mechanisms and their intermediate steps have been speculated about based on indirect evidence obtained from cyclic voltammetry and spectro-electrochemisty. We can now directly probe and predict the precise mechanistic details from first principles using our thermopotentiostat simulations. A corresponding snapshot for Ge(100) surfaces is shown in Fig. 2. Exceeding a potential drop of Φ0 > 2 V under anodic polarization, we observe that the reorientation of interfacial water is insufficient to screen the applied electric field. Instead, the interfacial dipole is screened by water dissociation, where H+ is released into the solvent and OH- groups adsorb on the surface (marked in orange). The subsequent discharge of the hydroxyl groups by the thermopotentiostat enables sustained reaction conditions for a continuous water splitting and electrooxidation of the surface.
These examples demonstrate how our continuous methodological advances help to reveal the elementary processes at electrified solid/liquid interfaces, enables us to show how idealised textbook models can be actually observed and revised, and thus achieve a truly microscopic understanding at the atomistic and electronic scales.
References
1. Surendralal, S.; Todorova, M.; Neugebauer, J.: Phys. Rev. Lett. 126 (2021) 166802.
2. Surendralal, S.: Todorova, M.; Neugebauer, J.: Phys. Rev. Lett. 120 (2018) 246801.
3. Deißenbeck, F.; Freysoldt, C.; Todorova, M.; Neugebauer, J.; Wippermann, S.: Phys. Rev. Lett. 126 (2021) 136803.