Variational Methods in Material Modeling: Applications of Hamilton’s Principle
The aim of modern material modeling is the realistic prediction of the behavior of materials and construction parts by numerical simulation. Experimental investigations prove that the microstructure and thus the mechanical properties may vary under loads. It is thus essential to describe the load-dependent microstructure in these cases by material models to close the system of fundamental physical equations. One elegant way for the derivation of such material models is given by the Hamilton principle which belongs to the class of variational, energy-based modeling strategies.
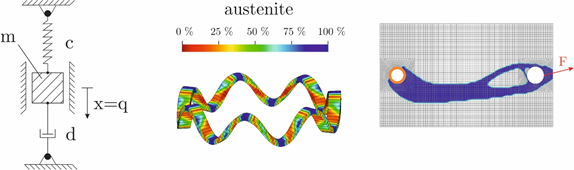
The talk starts with fundamental investigations for modeling the simple harmonic oscillator. Afterwards, the presented modeling concept is generalized to the Hamilton principle which is also applicable to deformable solids with evolving microstructure. As first example for such materials, phase transformations in solids are modeled. The numerical results are compared to experimental observations and an industrially relevant application is presented. In the last part of the talk, the universal character of the Hamilton principle is demonstrated by solving the inverse problem of topology optimization. To this end, a growth approach as observed in biological processes is presented which computes component structures with minimal weight at maximum stiffness.
Priv.-Doz. Dr.-Ing. Philipp Junker
Lehrstuhl für Mechanik-Materialtheorie der Ruhr-Universität Bochum
Geschäftsführender Gesellschafter der ComMaSIM UG (hb.)
Ruhr-Universität Bochum
Universitätsstr. 150, IC 03-713
44801 Bochum
| Phone | +49 234 32-26026 |
| Fax | +49 234 32-14154 |
Priv.-Doz. Dr.-Ing. Philipp Junker |
|
| Http | Priv.-Doz. Dr.-Ing. Philipp Junker |
| Lehrstuhl für Mechanik-Materialtheorie der RUB |