
The mechanical size effect as a mean-field breakdown phenomenon: Example of microscale single crystal beam bending
Single crystalline copper beams with thicknesses between 0.7 and 5 μm are manufactured with a focused ion beam technique and bent in a nanoindenter. The yield strengths of the beams show a mechanical size effect (smaller-is-stronger).
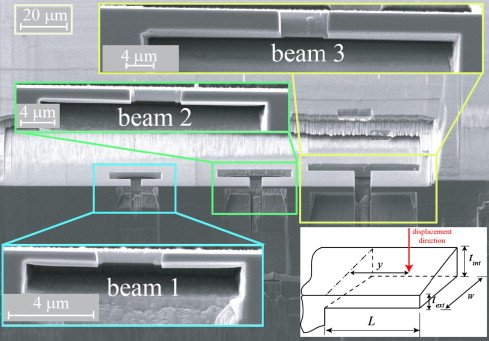
The geometrically necessary dislocation (GND) densities estimated from misorientation maps do not explain the observed size effect. Also, accumulation of GNDs principally requires pre-straining. We hence introduce a mean-field breakdown theory and generalize it to small-scale mechanical tests other than bending. The mean-field breakdown limit is defined in terms of a microstructural correlation measure (characteristic dislocation bow-out length) below which the local availability of dislocation sources and not the density of GNDs dominates the mechanical size effect. This explains why a size dependence can occur for samples that are not pre-strained (by using a very small critical strain to define the yield strength). After pre-straining, when GNDs build up, they can contribute to the flow stress. The mean-field breakdown theory can also explain the large scatter typically observed in small-scale mechanical tests as the availability of sufficiently soft sources at scales around or below the correlation length does not follow statistical laws but highly depends on the position where the probe is taken.
