4. Constitutive models
4.1. Introduction
The preceding section on kinematics discussed the multiplicative decomposition of the deformation gradient F :


As shown there the plastic deformation evolves as
and in case of dislocation slip as the only deformation process, according to equation (7) and using first order terms only, Lp can be formulated as sum of the shear rates on all slip systems

where vectors mα and nα are, respectively, unit vectors describing the slip direction and the normal to the slip plane of the slip system α; γ˙α is the shear rate on that same system. n is the number of (active) slip systems.
This section is about the constitutive equations that define these shear rates as a function of the external stress, σ, and the microstructural state of the material, S. In other words the kinematic formalism describes the geometrical aspects of the anisotropy of crystal mechanics without considering stresses while the constitutive equations capture the physics of the material behavior, in particular of the dynamics of those lattice defects that act as the elementary carriers of plastic shear. How the microstructural state of the material, S, is defined and how it evolves during loading depends on the kind of constitutive model used. In the following we present two classes of constitutive models, namely, phenomenological models and physics based models.
4.2. Phenomenological constitutive models
Phenomenological constitutive models mostly use a critical resolved shear stress, τcα , as state variable for each slip system α. Therefore, the shear rate, γ˙α, is formulated as a function of the resolved shear stress, τα = ![]()
![]() :, and that critical resolved shear stress:
:, and that critical resolved shear stress:

and the evolution of the material state is formulated as function of the total shear, γ, and the shear rate, ˙γα

One prominent group of examples for such a formulation is the one suggested by Rice [16], Hutchinson [240], Peirce et al. [27] and Peirce et al. [84] for face-centered cubic (fcc) metallic crystals. In this framework the kinetic law on a slip system is:

where ˙γα is the shear rate on slip system α subjected to the resolved shear stress τα at a slip resistance τcα; γ˙0 and m are material parameters that determine the reference shear rate and the rate sensitivity of slip, respectively. The influence of any slip system, index β, on the hardening behavior of a (fixed) slip system α is given by:

where hαβ is referred to as hardening matrix:

which empirically captures the micromechanical interaction among different slip systems. In this formulation h0, α, and τs are slip hardening parameters, which are assumed to be identical for all fcc slip systems owing to the underlying characteristic dislocation reactions. The parameter qαβ is a measure for latent hardening; its value is taken as 1.0 for coplanar slip systems α and β, and 1.4 otherwise, which renders the hardening model anisotropic. In the literature a number of variations of equations (16) and (17) can be found. Some authors [106] use the sinh function instead of a power law in equation (16), while others [88] use modified hardening laws like a generalized Voce equation [241, 242] instead of equation (17).
These types of kinetic formulations are currently the most frequently used ones in CPFE models although they suffer from the drawback that the material state is only described in terms of the critical resolved shear stress, τc, and not in terms of lattice defect populations [243, 244]. The latter approach, however, is required to render crystal plasticity models path-and size-dependent as will be discussed in the following.
4.3. Physics-based constitutive models
In contrast to the phenomenological constitutive models, the physically based ones rely on internal variables. In the case of plasticity the most important microstructural state variable certainly is the dislocation density as the dislocations are the carriers of plastic deformation2 . Models that treat the evolution of dislocation densities and calculate the flow stress from them have been proposed by various authors [19, 9, 232, 22, 24, 25]. In the following subsections we present the dislocation-based model by Ma et al. [23, 24, 25] in more detail. It should be noted, that even though the dislocations are the most important internal variable measure, more parameters are required for a full characterization of the microstructure, e.g. grain size and shape, second phase fractions, precipitate morphology, etc. However, only a few of these additional parameters have been introduced into dislocation-based CPFE models so far.
_________________
2It should be noted that in some models dislocation densities are calculated by using the Taylor relation (τ ∝ √ρ). These approaches must also be regarded as phenomenological models as they do not treat the evolution of the dislocation densitiess explicitly.
_________________
4.3.1. Dislocation-based constitutive laws in CPFE models
The dislocation density-based constitutive model introduced by Ma and Roters [23], Ma et al. [24] and Ma et al. [25] uses mobile dislocations, ραm , gliding along the slip system α to accommodate a part of the external plastic deformation. In order to do so they must overcome the stress field of the parallel dislocations, ραP, which causes the passing stress. Also they must cut P the forest dislocations, ραF, with the aid of thermal activation. In this framework we define the parallel dislocation density, ραP, and the forest dislocation density, ραF, for each slip system α in the following way: ραP are the dislo-FP cations parallel to the slip plane, and ραF are the dislocations prerpendicular to the slip plane. Considering the immobile dislocation density, ραSSD for fcc crystals the following projections can be used:
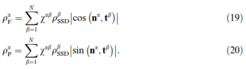
In these equations we introduce the interaction strength, χαβ, between different slip systems, which includes the self interaction strength, coplanar interaction strength, cross slip strength, glissile junction strength, Hirth lock strength, and Lomer–Cottrell lock strength. In this formulation only edge dislocations are considered owing to their limited mobility and tβ is their line direction.
In a dislocation-based model the Orowan equation typically serves as kinetic equation instead of equation (16) as it couples shear rates to mobile dislocations, i.e. it allows one to translate a continuum mechanical term into the physics of dislocations

where ρm is the density of mobile dislocations, b the magnitude of the Burgers vector and v the average velocity of the mobile dislocations. According to Ma and Roters [23] the mobile dislocation density can be calculated from the statistically stored dislocation density by a simple scaling law:

where T is the absolute temperature and B is given by

where kB is the Boltzmann constant and G the shear modulus; c1 to c3 are constants introduced in the dislocation density evolution laws below.
Under the assumption of forest cutting as the rate determining process, the velocity of the mobile dislocations can be calculated as:
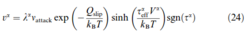
where λα is the jump width which is inversely proportional to the forest dislocation spacing, νattack is the attack frequency, Qslip is the effective activation energy for dislocation glide, and Vα the activation volume which can be calculated as:

with c3 being a fitting constant of order unity.
Finally, the effective shear stress ταeff can be calculated from the resolved shear stress and the passing stress as:
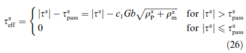
The phenomenological description of hardening in equation (17) is substituted by the evolution of the dislocation densities. For this purpose rate equations are formulated based on individual dislocation reactions. In [23] four such processes are taken into account, namely, lock and dipole formation as processes increasing the dislocation density and both, athermal and thermally activated annihilation as recovery processes. Detailed derivations of these rate equations can be found in [23]. In the following we summarize the results:
- Lock formation

- Dipole formation
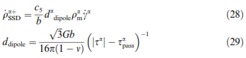
- Athermal annihilation

- Thermal annihilation due to climb of edge dislocations
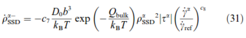
where c4,...,c8 are fitting constants, ddipole the critical distance for dipole formation, D0 the diffusion coeffcient, Qbulk the activation energy for dislocation climb and ![]() ref a reference shear rate.
ref a reference shear rate.
4.3.2. Introduction of geometrically necessary dislocations
Most of the constitutive laws reported in the literature can be attributed to the group of local models in which the total deformation gradient has been multiplicatively decomposed into elastic and plastic parts, and where the constitutive behavior can be fully described from the loading history. For stress–strain curves and texture predictions of polycrystals, local models have been shown to be powerful and effcient [108]. However, when the simulation scale becomes smaller such as in studies focusing on nanoindentation [170, 171, 174], micro-pillar compression [172], or small-scale beam bending [176], local models can be insufficient due to their inability to describe mechanical size effects.
The grain size dependence of the flow stress was first described by Hall and Petch by an empirical equation [245, 246]. Numerous studies have since then shown that the strengthening effect by a smaller grain size is due to a higher volume fraction of heterogeneous plastic deformation in the vicinity of grain boundaries. There are several explanations in the literature based on dislocation mechanisms such as pile-ups of mobile dislocations in front of the grain boundaries causing stress concentrations that increase the slip resistance or strain gradients near those interfaces. These strain gradients are assumed to produce an extra increment of dislocation densities which increase the slip resistance [20]. Beyond the grain size effect different types of microscale experiments (torsion, bending, indentation) have also revealed a length scale dependence of the flow stress [232]. In these experiments typically non-uniform plastic deformation occurs which may lead to orientation-and strain-gradients in the vicinity of a material point. These gradients can be associated with geometrically necessary dislocations (GNDs) [212]. In phenomenological models it is not straightforward how to integrate GNDs into the constitutive model. In contrast, in dislocation density-based models GND concepts can be easily integrated as part of the constitutive framework [210].
However, the calculation of strain gradients renders a constitutive model non-local which makes it more diffcult to implement. The main reason for this is that in a non-local model a material point is strongly coupled with its neighboring points during the evolution of GNDs. This means that strain gradient calculations have to converge for a set of neighboring material points in the same time increment. In order to achieve this some authors [26, 9] use the divergence theorem for formulating new differential equations using GNDs and SSDs as additional degrees of freedom for every node in an element. These algorithms require supplying additional boundary conditions for the dislocation density flux. While this is not complicated for simple calculations it is diffcult for complex load cases. An alternative and more general integration algorithm was therefore introduced by Ma et al. [24] to solve any non-local constitutive model in material subroutines such as offered by commercial FE solvers (e.g. Marc, Abaqus).
This section shows how GNDs can be introduced in the dislocation model presented above. As mentioned before Nye’s dislocation tensor [210] can be used to translate the strain gradient into GNDs3:

________________
3Λ is equal to the Nye tensor, α, introduced in section 3 divided by the magnitude of the Burgers vector, b; note however, that the notation here is different than in section 3.
________________
where the nabla operator ∇X is defined as the derivative with respect to the reference coordinate ∇X = ∂/∂X. Using equation (32) the resultant Burgers vector for an arbitrary oriented surface can be calculated. In general this tensor is non-symmetric with nine independent values. Therefore, the calculation of the exact GND content for every slip system requires additional assumptions as although there are 12 slip systems for the fcc crystal structure only 6 of them are geometrically independent [247].
Using the material time derivative of equation (32) in conjunction with equations (12) and (13), the change of the geometrically necessary dislocation density can be derived [24]

The integration of the GNDs into the constitutive model is now simply a matter of extending the projection into forest and parallel dislocations (equations (19) and (20)). To render this projection more convenient ![]() αGND is decomposed into three groups: one group of screw dislocations with tangent vector parallel to the slip direction dα, the other two groups of edge dislocations with tangent vectors parallel to nα and tα respectively
αGND is decomposed into three groups: one group of screw dislocations with tangent vector parallel to the slip direction dα, the other two groups of edge dislocations with tangent vectors parallel to nα and tα respectively
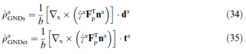
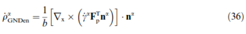
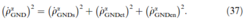
Equations (34) to (36) are a set of evolution equations for ρGND, just like those for ρSSD derived in the previous section. Finally the extended projection reads
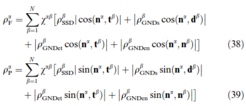
where absolute values of GNDs are used, so that the sings of their Burgers vectors are neglected. A direct result of this treatment is that no kinematic hardening can be predicted which is acceptable for single phase material and unidirectional loading.
4.3.3. Interface models
Grain boundaries act as obstacles to dislocation motion. At the onset of plastic deformation of polycrystals, mobile dislocations are first created on the slip system with the largest local resolved shear stress in the grain with the most favorable orientation. When encountering a grain boundary these mobile dislocations accumulate in front of that interface. Such events lead to stress concentrations at the interface that add to the external stress field at this material point. These micro-plastic effects, where the local arrangement of dislocations determines the local stress, cannot be treated one-to-one in a crystal plasticity continuum mechanical framework because such models map the underlying dislocation mechanics in a phenomenological statistical or even empirical form. However, homogenization is admissible at larger plastic strains where most of the slip activation processes can be captured by long-range stresses rather than by local ones [249]. This means that the dislocation mechanics can, beyond the micro-plastic regime, be homogenized in the form of statistical dislocation populations which in turn can be embedded as constitutive rate equations in a crystal plasticity theory [20, 19, 25].
Two approaches for including grain boundary mechanics into dislocationbased constitutive CPFE models can be found in the literature. In the first
type of models the grain boundaries are treated as being partially transparent to dislocations [25]. In the second type of models interfaces appear as perfect obstacles that do not allow dislocation penetration events [21]. The latter assumption can be implemented in FE simulations as an additional set of boundary conditions, namely, as a zero shear condition perpendicular to interfaces. While the latter approach appears to be relatively straightforward at first view it can be rather intricate when meshing complicated grain aggregates [85, 38, 14, 95]. As shown by Evers et al. [21] these additional boundary conditions result in an increased hardening of the material, however, they do not result in an increase of the initial yield stress, i.e. the Hall–Petch effect is not captured. In order to overcome this drawback Evers et al. [21] suggested to introduce grain boundary dislocations (GBD) as an initial content of GNDs at the position of the grain boundaries. These GBDs are calculated by Evers et al. [21] from the crystallographic misorientation across the interface in the following way: When considering two crystals with orientations QI and QII with slip systems (dα,β, tα,β, nα,β ), α,β =1, 2,..., 124, and a grain boundary with a normal vector nGB, which separates these two crystals (figure 9) one obtains the density of GBDs as
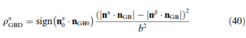
![Figure 9: Schematic drawing of penetration events for mobile dislocations through a grain boundary. The experimentally obtained micrograph is taken from the work of Shen, Wagoner, and Clark on steel [248]. Here lα', lβ', and lαGB are the tangent vectors of the dislocations, and bα, bβ, and bαGB are their Burgers vectors.](/3749658/original-1518446885.jpg?t=eyJ3aWR0aCI6MjQ2LCJvYmpfaWQiOjM3NDk2NTh9--5cf05457bb79794c5162b6d0040eba892d8e7cec)
______________________
4The indices α and β always refer to crystals I and II respectively.
______________________
The slip system β has to be chosen to minimize ραGBD. In the second type of approach Ma et al. [25] assume partial transparency of the interface to dislocations. The transmission probability of incoming mobile dislocations to penetrate a grain boundary can be treated in terms of an activation concept. The enthalpy for this activation process stems from the elastic energy that is required for the formation of misfit dislocations which remain as debris in the interface upon slip penetration. This activation enthalpy enters as an additional contribution into the activation term for the slip of mobile dislocations (equation (24)). It is likely that each transmission event will occur at the smallest possible energy consumption. This condition provides a selection criterion for the slip systems involved. The main task in this model, therefore, consists in identifying the outbound slip system on the other side of the boundary, which provides the closest geometrical match to the inbound slip system. The smallest misalignment between the active inbound and the expected outbound slip systems leads to the smallest possible energy barrier5.
___________________
5It is not actually checked whether or not this slip system can be activated by the local stress but it is anticipated as a likely situation as the outbound slip system orientation is close to the inbound one.
___________________
For an arbitrary transmission event, it is obvious that some incoming slip system does not, as a rule, match a corresponding one on the outbound side exactly, i.e. the shear is usually not coherent on the two sides of a grain boundary. Therefore, in order to meet the conservation of the lattice defect vector sum when crossing an interface, misfit dislocations will be created in the grain boundary. The additional energy required to produce such an extra misfit dislocation acts as an energy barrier for the thermally activated slip transmission event. This barrier, hence, acts as a penalty energy for such a situation. However, it should be interpreted in a somewhat more statistical manner. This means that it is not required to yield a strict one-to-one correlation between incoming and outgoing dislocations rather than a match in the overall shear on either side. Moreover, it is conceivable that the transmission event only rarely takes place owing to the local stiffening effect that it introduces. Along with this grain boundary hardening effect the accumulation of geometrically necessary dislocations in front of the interfaces acts as an additional stiffness effect. The mathematical treatment of this dislocation-based approach to grain boundary effects in the CPFE framework shown in Ma et al. [25] leads to the following equation for the penalty energy β that minimizes the activation energy,

where c'9 is a fitting constant, lα is the length of the incoming dislocation and Rα is geometrical factor describing the correlation of the incoming system α and the outgoing system β. It is worth to mention, that while the absolute magnitude of EαGB can be changed by the choice of c'9, the ratio of the activation energies for different boundaries is not affected by this value. As an example the activation energies of an incoming dislocation with a length b are calculated for twist boundaries which are characterized by rotations about the [111] and [110] crystal directions, respectively, under the additional constraint, that the grain boundary plane is perpendicular to the rotation axes. The calculations apply for the fcc crystal structure. The results are shown in figures 10 and 11, where the activation energy has been normalized by the factor ½Gb3 and the constant c'9 was chosen to be equal to one. Both figures show also the average of the energy barrier for better comparison. From these curves it is clear, that a grain boundary is a strong obstacle to dislocation motion, as the average activation energies for the formation of the misfit dislocations easily reach the order of magnitude of the activation energy for cutting forest lattice dislocations.
![Figure 10: Normalized activation energy for a twist grain boundary with rotations about the [111] direction using c'9 = 1 in equation (41). The normalization factor is ½ Gb3.](/3748565/original-1518438009.jpg?t=eyJ3aWR0aCI6MjQ2LCJvYmpfaWQiOjM3NDg1NjV9--14502080cc77e1e852489349332aba906937f21a)
Figure 10: Normalized activation energy for a twist grain boundary with rotations about the [111] direction using c'9 = 1 in equation (41). The normalization factor is ½ Gb3.
![Figure 11: Normalized activation energy for a twist grain boundary with rotations about the [110] direction using c'9 = 1 in equation (41). The normalization factor is ½Gb3.](/3748576/original-1518438009.jpg?t=eyJ3aWR0aCI6MjQ2LCJvYmpfaWQiOjM3NDg1NzZ9--8f4f0f04c2dc9fd1e65a86df90636d2e0473bc94)
Figure 11: Normalized activation energy for a twist grain boundary with rotations about the [110] direction using c'9 = 1 in equation (41). The normalization factor is ½Gb3.
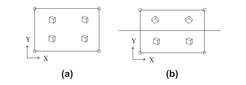
Figure 12: 2D schematic drawing of the bulk element (a) and of the grain boundary element (b) for the initial case. During the deformation, for the bulk element GNDs should keep the continuity of the lattice in X and Y directions, while for the grain boundary element the lattice continuity is only kept in X direction. In Y direction the penetration energy is introduced.
It is observed that the energies for slip penetration are periodic. This effect arises from the octahedral symmetry of the slip systems in the crystal. The activation energy for the penetration shows a complicated relationship with the misorientation especially when the rotation angle is larger than about 20°. One can see, that the energy barrier strongly depends on the misorientation of the two crystals. However, the average activation energies show a much more constant behavior, which implies that the strong effects for single slip systems will be averaged out to some extend in macroscopic experiments.
In most CPFE implementations grain boundaries coincide with element boundaries. In the dislocation-based approach discussed above a special type of bi-material element across the grain boundary is introduced. In this element one half of the Gauss points belongs to one crystal, while the other one belongs to the other crystal, see figure 12. In this new type of element one can use a modified version of equation (24), namely
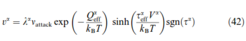
where Qαeff is the modified effective activation energy

When comparing this equation with the one specified in section 4.3.1, the only difference is the use of Qαeff instead of Qslip. According to equation (41) the energy QαGB is calculated by finding the outgoing slip system β that GB minimizes it:
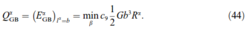
where c9 is a dimensionless fitting parameter which is a function of c'9 and the grain boundary element thickness LGB.


























![Figure 9: Schematic drawing of penetration events for mobile dislocations through a grain boundary. The experimentally obtained micrograph is taken from the work of Shen, Wagoner, and Clark on steel [248]. Here lα', lβ', and lαGB are the tangent vectors of the dislocations, and bα, bβ, and bαGB are their Burgers vectors. Figure 9: Schematic drawing of penetration events for mobile dislocations through a grain boundary. The experimentally obtained micrograph is taken from the work of Shen, Wagoner, and Clark on steel [248]. Here lα', lβ', and lαGB are the tangent vectors of the dislocations, and bα, bβ, and bαGB are their Burgers vectors.](/3749658/original-1518446885.jpg?t=eyJ3aWR0aCI6MzQxLCJmaWxlX2V4dGVuc2lvbiI6ImpwZyIsIm9ial9pZCI6Mzc0OTY1OH0%3D--a96200acf10933edd2e461ec630d6ce649f28cbd)

![Figure 10: Normalized activation energy for a twist grain boundary with rotations about the [111] direction using c'9 = 1 in equation (41). The normalization factor is ½ Gb3. Figure 10: Normalized activation energy for a twist grain boundary with rotations about the [111] direction using c'9 = 1 in equation (41). The normalization factor is ½ Gb3.](/3748565/original-1518438009.jpg?t=eyJ3aWR0aCI6MzQxLCJmaWxlX2V4dGVuc2lvbiI6ImpwZyIsIm9ial9pZCI6Mzc0ODU2NX0%3D--266af67066fc4829900a23a3382800cb56d04fa3)
![Figure 11: Normalized activation energy for a twist grain boundary with rotations about the [110] direction using c'9 = 1 in equation (41). The normalization factor is ½Gb3. Figure 11: Normalized activation energy for a twist grain boundary with rotations about the [110] direction using c'9 = 1 in equation (41). The normalization factor is ½Gb3.](/3748576/original-1518438009.jpg?t=eyJ3aWR0aCI6MzQxLCJmaWxlX2V4dGVuc2lvbiI6ImpwZyIsIm9ial9pZCI6Mzc0ODU3Nn0%3D--c235c3f9372e763f8fe4a6a7a8ccef4bce44e096)



