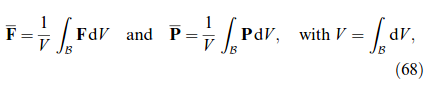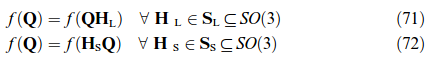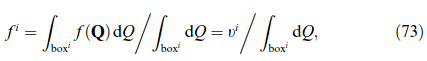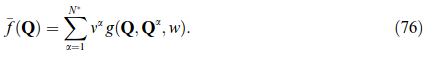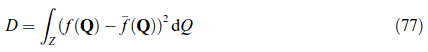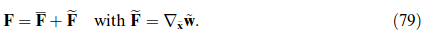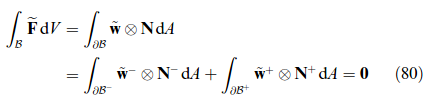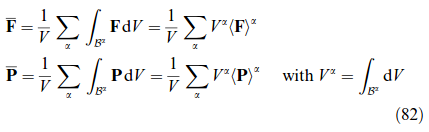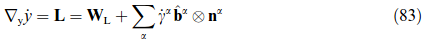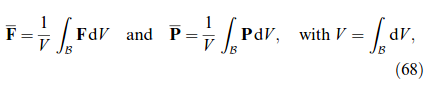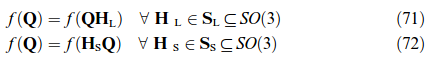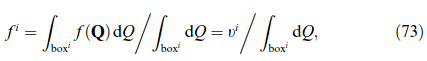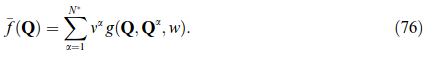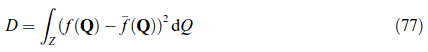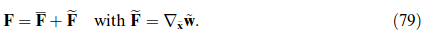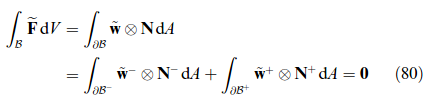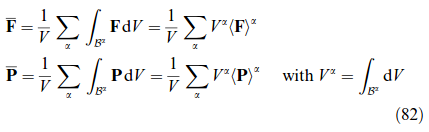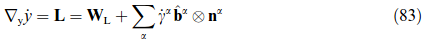6. Homogenization methods in CPFE analysis

6.1. Introduction

In contrast to the direct crystal plasticity method of modeling aggregates of grains one-to-one, finite element analysis is often used to predict the mechanical behavior of engineering structures. This is typically done at the component or design scale using homogenized material properties (indicated by an overbar). At the continuum scale, material points in the reference configuration B ⊂ R³ are projected by the non-linear deformation map onto points in the current configuration . The corresponding tangent map or deformation gradient is then given by . In order to derive the work-conjugate stress (first Piola–Kirchhoff stress) and solve the equilibrium conditions within the finite element analysis a constitutive law which connects to is required. However, a direct formulation of is in general difficult to impossible, since the mechanical response of (metallic) materials is determined by their underlying microstructure. This microstructure cannot be regarded as a homogeneous continuum but it typically contains grains with differing properties. As a rule in engineering parts the grain scale is orders of magnitude smaller than the component scale, thus ruling out the possibility to include all degrees of freedom presented by a huge grain aggregate. Therefore, a two-level approach is pertinent. Each material point is linked to a domain B ⊂ R³ containing a finite number of microstructure constituents, e.g. grains, for which the individual constitutive behavior can be modeled, i.e. the constitutive relation between P and F is known. This constitutive relation is in general dependent on the state of the material, most notably on its thermo-mechanical history. Since the macroscopic quantities and are related via the volume averages

to the corresponding microscopic quantities F and P inside B, this “numerical zoom” shifts the constitutive assumptions between and from the macroscale to the micro-scale.

The term “homogenization” now refers to the transition between the micro-scale and the macro-scale defined in a general fashion by equation (68). In physics such procedures are also referred to as coarse graining. In the next section we first review methods of how to select grain aggregates in each domain B such as to ensure that they reflect the overall crystallographic texture of the material in question in a statistically representative way. After this, the following sections outline three routes which are mainly followed when it comes to the homogenization of viscoplastic polycrystalline materials in the framework of component scale finite element analysis.

6.2. Statistical representation of crystallographic texture

Crystallographic texture is quantified by the crystallite orientation distribution function (CODF) which defines the probability f(Q) that a volume fraction, dV/V , of the polycrystalline aggregate is taken up by crystallites falling into an infinitesimal neighborhood around orientation Q:

The crystal orientation is described by a proper orthogonal matrix Qij = gi ej ∈ SO(3) which maps the reference basis e onto the crystal basis g. Using the notation introduced by Bunge [293], i.e. parameterizing Q by Euler angles {ϕ1, φ, ϕ2}, the infinitesimal volume, dQ, of orientation space follows as:

The normalization factor of 1/8π2 arises due to the requirement that ƒdV/V ≡ 1. (Note that f(Q) ≡ 1 for a random texture.) The orientation distribution reflects any symmetry present in the crystal lattice and/or the sample geometry. This implies the following symmetry relations:

with SL and SS being the symmetry group of the lattice and sample, respectively. Therefore, the CODF is fully determined from f(Q) within any one of the independent regions of Euler space (also addressed as fundamental zones) resulting from equations (71) and (72).

For practical reasons, the CODF is frequently stored in a discrete fashion by subdividing the fundamental zone Z of Euler space into N boxes of equal angular extension—typically 5 × 5 × 5 cubic degrees—and recording discrete values, fi, for each box. Ideally,

i.e. the fi values correspond to the CODF average within the i^th box with volume vⁱ .

The task now consists of selecting a finite number, N∗, of discrete orientations such that the overall texture is still represented as accurately as possible by the limited set. Depending on the requirements of the intended simulation, the individual volume fractions assigned to each selected orientation may be either equal or differ from one another.

With respect to the first option, Eisenlohr and Roters [228] recently combined a deterministic scheme with a probabilistic scheme to sample a given number of equally-weighted orientations from a discrete CODF. While the probabilistic scheme accepts a randomly chosen orientation in proportion to the respective value of fi, the deterministic part is based on the integer

which gives the number of times the orientation i should be selected into the representative set. To yield an overall set of N^∗ samples the constant C has to be iteratively adjusted to fulfill

This iterative procedure is easily solved, for instance, with a binary search algorithm in a matter of seconds on a standard single-CPU computer. Regarding reconstruction quality, it could be demonstrated that for N^∗ > N the set resulting from equations (74) and (75) is much closer to the original CODF than probabilistic sets using vⁱ as probability to include orientation i (see equation (73)). However, for N^∗ < N a systematic over-weighting of the large original vⁱ, and thus pronounced sharpening of the reconstructed texture, is observed. To overcome this inherent problem, the deterministic method is modified as follows: if the requested number, N^∗, of sampled orientations is less than the number of boxes in the (fundamental zone of the) original CODF, i.e. if N^∗ <N, one nevertheless generates a population of N discrete orientations according to Eqs. (74) and (75) but then selects a random subset containing only the requested N^∗ ∗/N.

Melchior and Delannay [184] tackled the problem of assigning orientations to an aggregate of N^∗ differently sized grains which constitute a representative volume element. They started from a large set of probabilistically selected, equally-weighted orientations [227] and introduced an algorithm to divide this set into N^∗ collections of similar orientations. Each collection represents a single grain (of average orientation) and comprises as many orientations as is required to match the respective volume fraction of this grain. By allowing this additional degree of freedom in the relative weight of assigned (average) orientations, the reconstruction quality resulting from a fixed number of orientations can be dramatically increased in comparison to equal-weight probabilistic sampling.

Böhlke et al. [294] presented a possible solution to the problem of approximating the CODF by a random background plus a small and fixed number of texture components of variable weight. First, a grid of equal angular extension in {ϕ1, φ, ϕ2} is constructed within the fundamental zone. An approximation then results from superposition of (at most) N^∗ von Mises–Fisher distributions, g(Q, Q^α, w), each centered on a distinct grid point Q^α with fixed half-width w:

The difficulty arises from selecting appropriate Q^α out of the available grid points and assigning respective variable weights ν^α such that the distance

between original CODF and its approximation is minimized. This corresponds to a mixed integer quadratic programming (MIQP) problem for which robust solvers exists.

6.3. Computational homogenization

Within each region B containing a microstructure attached to a certain material point  one defines the deformation map y(x): x ∈ B → y ∈ S which translates the reference configuration B of that microstructure to its current configuration S. The associated deformation gradient is given by F = ∇y. The deformation map is expressed as the homogeneous deformation , inherited from the material point, and a superimposed fluctuation field :

Thus the microscopic and macroscopic deformation gradients are related by

Combining equations (79) and (68) results in the constraint that the deformation gradient of the fluctuation field vanishes on average:

The three equivalent integral terms of equation (80) indicate the three possible boundary conditions of different rigorousness. One might rule out any fluctuations at all, i.e. = 0 in B (i). However, homogeneous boundary conditions i.e. = 0 on ∂B (ii), also satisfy equation (80). Still more relaxed (periodic) boundary conditions are possible if the boundary is decomposed into two opposite parts ∂B = ∂B⁻ ∪ ∂B⁺ with ∂B⁻ ∩ ∂B⁺ = ∅. Periodicity of the domain B is then assured by requiring for each point x⁺ ∈ ∂B⁺ , that the associated point x⁻ ∈ ∂B⁻ has an opposite normal N⁺ = −N⁻ and equal values of the fluctuation field ⁻ = ⁺ (iii). Thus the degrees of freedom offered to the microstructure inside B, and hence its compliance, increase from condition (i) to (iii). For the micro-continuum a static equilibrium is assumed, which, in the absence of body forces, is governed by the field equation

Computational homogenization now refers to the numerical solution of the boundary value problem in posed by equations (79) and (81) in connection with a constitutive relationship P(F) per individual phase. For this solution, in general, a number of techniques can be employed. The majority of recent contributions discretized the boundary value problem by means of the finite element method, see e.g. [295, 113, 296, 297, 298], or using a Fourier series approach on a regular grid [299, 300]. In addition, the boundary element method or meshless schemes are equally applicable.

6.4. Mean-field homogenization

Within the mean-field approach the microstructure present in the domain B is considered as a system of inclusion(s) in a matrix. Here, the boundary value problem outlined in the preceding section is not solved rigorously, but only in a volume-averaged sense. This means, that the spatial variation in P and F is not resolved anymore, thus only spatially averaged quantities per phase α are considered. Hence, macroscopic quantities valid for the material point equal the volume-weighted sum of the respective quantities over all microstructural constituents. The mean-field counterpart of equation (68) then reads:

The most basic assumptions regarding the partitioning of stress or strain would be either uniform stress (P)^α = or uniform deformation gradient ()^α = among all phases/grains α =1,...,N present in the microstructure. These extremal cases were introduced by Reuss [301] and Voigt [302] for elasticity. The full constraints Taylor [4] assumption corresponds to uniform strain in the case of plasticity. Both assumptions disregard the shape and local neighborhood of the inclusions and generally violate compatibility and equilibrium, respectively. More sophisticated assumptions make use of the solution to the problem of an elastic ellipsoidal inclusion in an infinite elastic matrix given by Eshelby [303]. A recent review of the by now well established laws which govern the strain partitioning in a linear elastic composite has been given by Nemat-Nasser and Hori [304]. Out of those, the most frequently employed are the self-consistent approach originally suggested by Kröner [305] and the scheme introduced by Mori and Tanaka [306] (see also [307]). In the former, each inclusion is treated like an isolated one within a matrix having the (unknown) overall stiffness of the composite. The latter embeds each inclusion into the original matrix but considers the average matrix strain to act as far-field strain on the overall composite.

However, extension of such homogenization schemes from the linear to the non-linear case is facing difficulties, most importantly, since the stiffness, i.e. strain(rate)-sensitivity of stress, is typically inhomogeneous for a given phase due to its heterogeneous strain. The stiffnesses are usually homogenized by using the average strain per phase as a reference input into the respective constitutive law. In order to establish a link between stress and strain per phase, secant (connecting total stress to total strain) and tangent (connecting stress increments to strain increments) formulations for the moduli are employed. The latter has some advantages since it is not restricted to monotonic loading and generally performs better for anisotropic material behaviour. Hill [308] originally introduced this incremental scheme together with a self-consistent approach. Lebensohn and Tomé [309] later proposed a self-consistent integral formalism which links total stress to strain rate. Further self-consistent schemes are, e.g., due to Berveiller and Zaoui [310] who employed a secant modulus tensor while Masson et al. [311] proposed an affine formulation. Recent developments in the incremental tangent formalism can be found, for instance, in [312] and [313].

6.5. Grain-cluster methods

Grain-cluster models are an intermediate approach between the meanfield schemes and spatially resolved solutions of a representative volume element outlined above. They reduce the high computational cost of the latter by restricting the degrees of freedom to a small number of regions with (typically) homogeneous strain inside each zone. Those regions are identified with grains or parts of grains, thus extending the mean-field approaches by taking into account direct neighbor–neighbor interactions among the constituents of a (multiphase) polycrystal. The introduction of grain aggregates now allows relaxation of the assumption of homogeneous strain in each constituent (Taylor)—which generally led to an overestimation of the polycrystalline strength and rate of texture evolution—by enforcing compatibility only in an average sense for the aggregate as a whole.

The basic concept of a partial relaxation of the Taylor hypothesis has been presented in the works of Van Houtte [314, 315], Honneff and Mecking [316], and Kocks and Chandra [317].

In his LAMEL model Van Houtte [314, 315] considers a stack of two grains subjected to an imposed velocity gradient

which is accommodated through lattice rotation W_L and crystallographic γ^α bˆ^α slip on systems α slipping at shear rates of γ˙^α bˆ^α. is the unit vector along the slip direction of system alpha. In each of the two grains—connected by an interface with normal n—the local (homogeneous) velocity gradients l and l^b are allowed to deviate from the global one by a number of “relaxation” (shear) modes K^r that do not alter n:

Depending on assumptions of the grain shape, typically one or two relaxation modes are considered. In the case of an interface normal along the macroscopic x3 direction and for grains which are flat along n = (001), two relaxation modes are considered where the only non-zero component in K¹ is K¹₃₁ = 1 and in K² is K²₃₂ = 1. By distributing the shear relaxation in a symmetric fashion (see equations (84) and (85)), the bicrystal as a whole fulfills the Taylor hypothesis; however, locally different slip systems can be active.

The activity of the real slip systems α and those attributed to the relaxation modes r are determined by minimizing the plastic dissipation

with suitably chosen penalty terms for each τ^r .

A certain drawback of the original LAMEL model consists in its restriction to deformation modes which are compatible with the presumed grain aspect ratio, e.g. pancake-like grains in rolling. This restriction is overcome by two recent models [20, 318] which focus on the boundary layer in between two neighboring grains. Both models apply a relaxation in the plane of the grain boundary (having normal n). The ALAMEL model, introduced by Van Houtte et al. [318], symmetrically relaxes two local velocity gradient components among the neighboring grains such that ∑_r K^r = a ⊗ n with a ⊥ n. This is identical to the LAMEL case of pancake grains discussed above. As a result, stress equilibrium at the boundary is maintained except for the normal component [318]. The relaxation proposed by Evers et al. [20] is slightly different, as they, firstly, symmetrically relax the deformation gradient on both grains by ΔF = ±a ⊗ n, and secondly, determine the components of a by prescribing full stress equilibrium at the grain boundary, which is equivalent to a minimization of deformation energy. A real grain structure can then be mimicked by enclosing each grain with bicrystalline contacts towards its neighbors. The distribution of interface orientations reflects the (evolving) grain morphology thus decoupling grain shape from the deformation mode under consideration.

An extension of the mono-directional, thus anisotropic, two-grain stack considered in above mentioned LAMEL model to a tri-directional cluster of 2 × 2 × 2 hexahedral grains is due to Crumbach et al. [319] based on former work by Wagner [320]. In this scheme, termed grain interaction (GIA) model, the overall aggregate is subdivided into four two-grain stacks with the stacking direction aligned with the shortest grain direction j' and another set of four stacks with the stacking direction aligned with the second-shortest grain dimension j'' . Relaxation of E_ij] (i =1, 2, 3) and E_ij'']] (i ≠ j') is performed in the spirit of LAMEL, i.e., via mutually compensating shear contributions of both stacked grains, such that each two-grain stack fulfills the external boundary conditions—and in consequence the cluster as a whole. To maintain inter-grain compatibility—possibly violated by different strains in neighboring stacks—a density of geometrically necessary dislocations is introduced, which forms the basis for the evaluation of the mismatch penalty energy in equation (86). The profound progress of the GIA approach is that it connects the inter-grain misfit penalty measure to material quantities such as the Burgers vector, shear modulus, work-hardening behavior, and grain size. The GIA model formulation is compatible with arbitrary deformation modes and is, hence, not confined to plane strain. It was recently used in conjunction with a finite element solver where it served as a texture-dependent homogenization model [321].

6.6. Guidelines for implementing homogenization models in CPFE frameworks

This section presented different types of homogenization concepts. They all have the common aim to describe the local mechanical interaction of clusters of crystals (including also different phases if required) that are jointly exposed to fixed boundary conditions. Relaxations may occur inside these clusters depending on model complexity.

It must be emphasized that no homogenization model is principally correct or incorrect. For instance the use of an equal-stress hypothesis (same stress in all grains) can be sensible when two sequentially arranged crystals are stressed and a Taylor–Bishop–Hill hypothesis (same strain in all grains) may be adequate when two crystals are arranged parallel to each other and are jointly exposed to the same displacement. This means that the homogenization model may be chosen according to the expected boundary conditions. Even simple homogenization models can provide decent results for certain loading situations while failing for others.

Another important aspect in selecting the right homogenization model is the property that is to be predicted. For instance the simulation of certain microstructure features such as grain misfit quantities (e.g. GNDs), internal strains, or crystallographic textures typically require a higher level of detail in the underlying homogenization model than the prediction of a polycrystal flow curve.

An essential step in the development and implementation of homogenization models is the validation procedure. According to the experience of the authors the best way to test homogenization models lies in the prediction of crystallographic textures. The reason for this recommendation is that first, deformation-induced texture changes are very sensitive to model and boundary condition details and second, textures can be quantitatively measured and compared one-to-one with corresponding predictions. Homogenization models that predict wrong textures will most likely also predict wrong mechanical properties. In contrast, a model providing satisfying mechanical result does not necessarily predict correct textures.

Finally, it is an obvious requirement that the chosen homogenization model must be suited for the size of the simulated part in order to reduce computation time to a reasonable level.