Phase Diagram of Grain Boundary Facet and Line Junctions in Silicon
Faceting of grain boundaries has a strong impact on the properties of structural, functional, and optoelectronic materials. In this project, we employ density-functional theory and modified embedded atom method calculations to investigate the energetics and thermodynamic stability of facets and line junctions in Silicon. We find that higher energy metastable GB phases can be stabilized by thermodynamics and not kinetics when constituting the facets at line junctions. This is in contrast to the common perception that the properties of faceting are merely driven by the anisotropic GB energies.
Σ3 tilt GBs in Si is a family of interfaces with special fundamental and technological interest, e.g. Σ3 GBs constitute up to 80% of GBs in Si ignots grown by dendritic casting. The Σ3{111} twin boundaries have negligible boundary energy and are electrically inactive and hence are preferred over other electrically active boundaries. However, the Σ3{112} GBs exist it two stable/metastable states, the higher energy symmetric (S-Σ3) and the lower energy asymmetric (A-Σ3). Moreover, the {111} and {112} boundaries are also formed by the dissociation of higher Σ value GBs. The facet junctions of the TB with the A-Σ3 show a unique anisotropic segregation mechanism, that goes beyond the classical picture of planar McLean type segregation1. Nevertheless, the driving force that causes faceting in these system, i.e., energetics, kinetics, and/or impuritity segregation, is an open issue.
In the present project we employ density functional theory (DFT) and large scale modified embedded atom method (MEAM) potential calculations and we investigate the structure, energetics and strain associated with these boundaries. Based on the our DFT calculations we parametrize a MEAM potential suitable to describe GB energetics and long range elastic interactions in Si. Our calculations revealed that Σ3 tilt GBs with the [110] rotation axis are intrinsically unstable against faceting towards {111} and {112} facets.
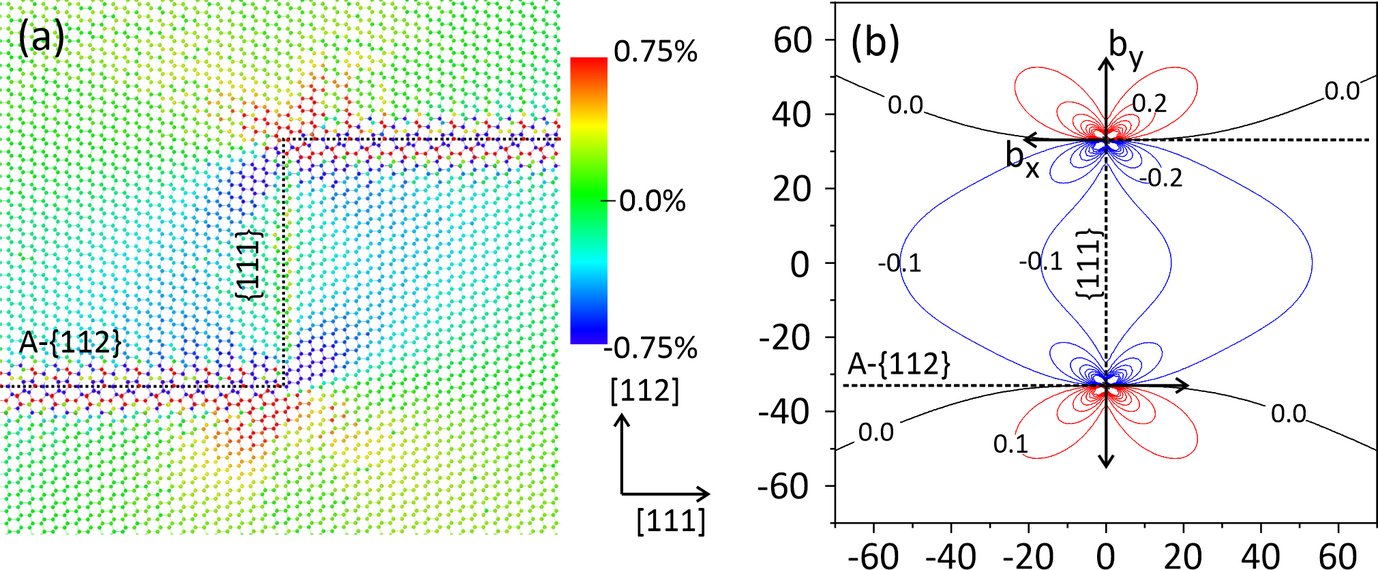
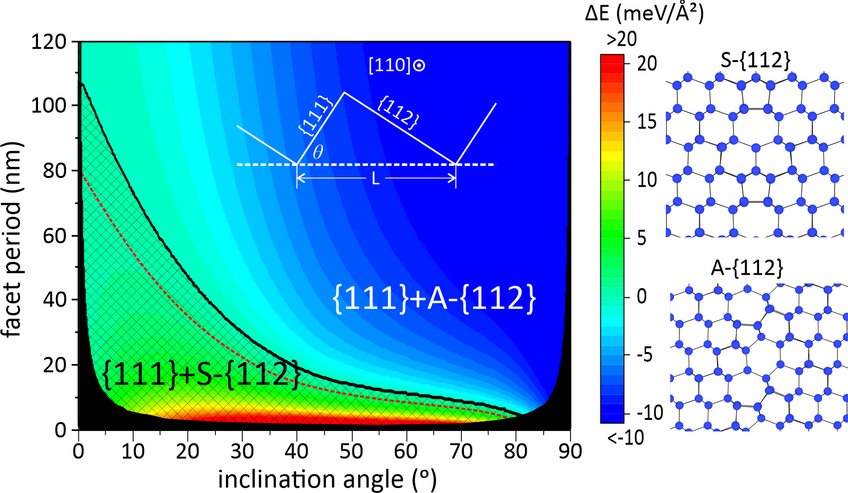
Furthermore, based on aforementioned calculations we construct a facet and line junction phase diagram that describes and predicts the reconstructions of these extended defects as function of facet length and boundary inclination angle. This diagram reveals that large (small) inclination angles with respect to {111} plane and/or large (small) facet lengths favor junctions with A-Σ3 (S-Σ3) facets, respectively. This is explained in terms of (i) the large anisotropy in the energies of S- and A-Σ3 and (ii) the presence (lack) of extended defects at the {111} and A- (S-) {112} line junctions, respectively: While the low energy of the A-Σ3 facets favors these boundaries over their symmetric counterparts, line junctions of twin boundaries with A-{112} facets are accommodated by edge type dislocations. The long range interactions constitute these facets highly unfavorable at small facet lengths. On the other hand, S-Σ3 are commensurate to the Σ3 coincidence site lattice and the energy of the corresponding faceted junction is independent of the facet length.
These findings shed light upon GB faceting phenomena and have important implications on the GB mobility mechanisms, the electronic properties as well as on selective impurity segregation at line junctions and facets in mc-Si: At large inclination angles the A-Σ3 GBs will adopt the maximum length allowed by the microstructure and grain size. Furthermore, the highly strained core region and its topology at the line junctions will strongly influence impurity segregation at these regions. On the other hand, at small inclination angles, the deep states introduced by the S-Σ3 facets will act as a recombination centers and will be detrimental for the device efficiency.
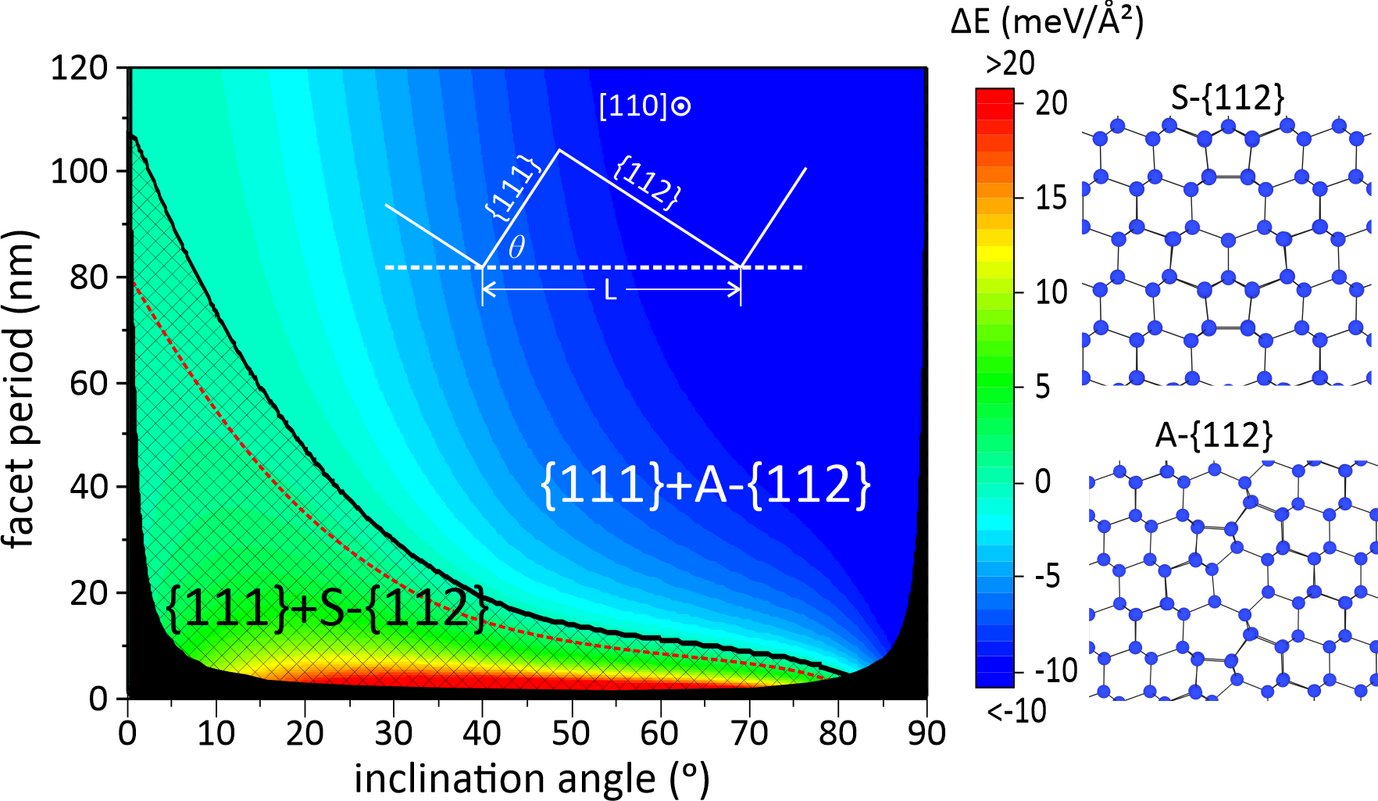
These findings shed light upon GB faceting phenomena and have important implications on the GB mobility mechanisms, the electronic properties as well as on selective impurity segregation at line junctions and facets in mc-Si: At large inclination angles the A-Σ3 GBs will adopt the maximum length allowed by the microstructure and grain size. Furthermore, the highly strained core region and its topology at the line junctions will strongly influence impurity segregation at these regions. On the other hand, at small inclination angles, the deep states introduced by the S-Σ3 facets will act as a recombination centers and will be detrimental for the device efficiency.