5. Displacive phase transformations in CPFE modeling
5.1. Introduction
The preceding sections focused on dislocations as carriers of plastic shear. However, materials such as austenitic steels, TRIP steels (TRIP: transformation induced plasticity), brass, TWIP steels (TWIP: twinning induced plasticity), and shape memory alloys, deform not only by dislocation slip but also by displacive deformation mechanisms (also referred to as displacive transformations). These mechanisms are characterized by a dffusionless collective motion of clusters of atoms where each atom is shifted only by a small distance relative to its neighbors. Such transformations create shears with kinematics similar to that of dislocations. Two such mechanisms and their incorporation into the CPFE framework will be discussed here, namely, martensite formation [74, 80] and mechanical twinning [164, 165, 166, 169]. Martensite formation takes place by a shear-induced change of the crystal structure which, as a rule, involves a volume change. Mechanical twinning proceeds by a shear mechanisms which reorients the volume affected into a mirror orientation relative to the surrounding matrix. We discuss how the CPFE approach can be modified to include these mechanisms and how the interactions among the competing shear carriers can be considered in the constitutive formulations.
5.2. Martensite formation and transformation-induced plasticity in CPFE
The presence of metastable retained austenite grains is responsible for the strength–ductility characteristics of transformation-induced plasticity (TRIP)assisted multiphase steels [250]. Upon mechanical and/or thermal loadings, retained austenite may transform into martensite and generate the TRIP effect. The investigation of the TRIP effect was initiated by Greenwood and Johnson [251] in 1965, where in a test specimen, irreversible plastic deformations were observed at a stress lower than the theoretical yield stress of the material. It has been suggested that the additional plastic deformation of the material is induced by the volumetric growth accompanying the transformation of retained austenite into martensite (see, e.g., Fischer et al. [252]). In the same year, Patel and Cohen [253] observed that during transformation, martensite develops in a preferred orientation that maximizes the transformation driving force.
Wechsler et al. [254] proposed a crystallographic model for the kinematics of martensitic transformations. This concept was refined by Ball and James [255], who further developed the modeling concept within the energy minimization landscape. During the last decades, various constitutive models for martensitic transformations have been proposed, such as the onedimensional model of Olson and Cohen [256], which was extended into a three-dimensional model by Stringfellow et al. [257]. Lately, more complex micromechanical models were proposed, e.g., [83, 258, 259, 260, 67, 68, 69, 75, 70, 71, 72, 73, 261, 262], which have been used in particular for simulating TRIP steels. However, the models mentioned above have some drawbacks, i.e., most of them were derived for a small-strain framework This can lead to inaccurate predictions as martensite transformations induce locally large elastic and plastic deformations, even if the effective macroscopic deformation is relatively small. Furthermore, an isotropic elasto-plastic response is often assumed. This constraint is quite strong, especially at the single crystal scale, where the effect of crystallographic anisotropy cannot be neglected.
The following sections present the development of a crystallographicallybased thermo-mechanical model for simulating the behavior of multiphase TRIP-assisted steels. The austenitic phase is described by a single crystal elasto-plastic-transformation model.
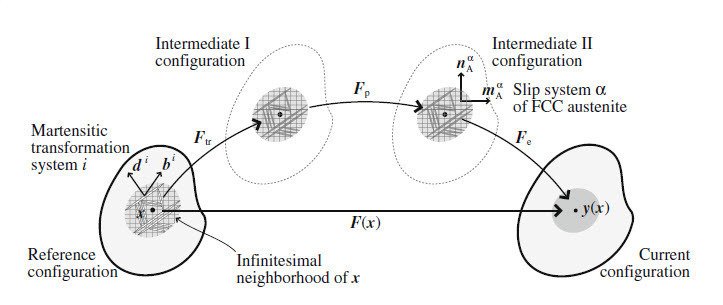
The phase transformation model of Suiker and Turteltaub [263, 78, 234] is applied to simulate the transformation of face-centered cubic (fcc) austenite into body-centered tetragonal (bct) martensite. This model is developed within a multi-scale framework and uses the results from the crystallographic theory of martensitic transformations [254, 255]. The martensitic transformation model is coupled to a single crystal plasticity model for fcc metals in order to account for plastic deformation in the austenite. The coupling between the transformation and plasticity models is derived using a thermodynamically-consistent framework.

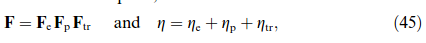
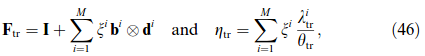
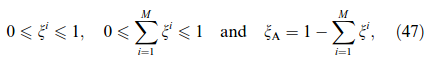




![Figure 14: Under an applied stress, one half of the initial volume (dashed lines) shears to form a twin (solid lines) (after Hirth and Lothe [269])](/3748829/original-1518438013.jpg?t=eyJ3aWR0aCI6MTM3OCwib2JqX2lkIjozNzQ4ODI5fQ%3D%3D--218481c319c3c92de1fbb91b33f03a3010b78d2c)
![Figure 15: Schematic representation of the three configurations and the corresponding decomposition of the deformation gradient F into elastic and plastic contributions, modified by Kalidindi to account for mechanical twinning [114,164].](/3748962/original-1518446869.jpg?t=eyJ3aWR0aCI6MTM3OCwib2JqX2lkIjozNzQ4OTYyfQ%3D%3D--26a8f8c23bfaac64c0aee3c77dd0a1e8e52b5591)

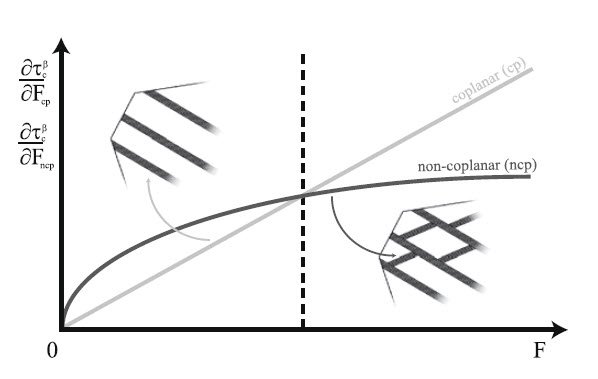


















![Figure 14: Under an applied stress, one half of the initial volume (dashed lines) shears to form a twin (solid lines) (after Hirth and Lothe [269]) Figure 14: Under an applied stress, one half of the initial volume (dashed lines) shears to form a twin (solid lines) (after Hirth and Lothe [269])](/3748829/original-1518438013.jpg?t=eyJ3aWR0aCI6ODQ4LCJmaWxlX2V4dGVuc2lvbiI6ImpwZyIsIm9ial9pZCI6Mzc0ODgyOX0%3D--26ff53b251ca09bf25fe497c1d992969d64ca5c2)



![Figure 15: Schematic representation of the three configurations and the corresponding decomposition of the deformation gradient F into elastic and plastic contributions, modified by Kalidindi to account for mechanical twinning [114,164]. Figure 15: Schematic representation of the three configurations and the corresponding decomposition of the deformation gradient F into elastic and plastic contributions, modified by Kalidindi to account for mechanical twinning [114,164].](/3748962/original-1518446869.jpg?t=eyJ3aWR0aCI6ODQ4LCJmaWxlX2V4dGVuc2lvbiI6ImpwZyIsIm9ial9pZCI6Mzc0ODk2Mn0%3D--381db450a05c454a6c8ee4cea70c6c496e919354)




