Limits of Empirical Supercell Extrapolation
The supercell approach allows to model defects with efficient periodic boundary models. By making the supercell sufficiently large, in principle, the limit of an single defect can be recovered. In practice, defect-defect interactions are still relevant for affordable system sizes. We demonstrate that empirical extrapolation has its limitations if the underlying physics is not taken into account or not even known.
Most crystal defects such as missing atoms (vacancies) or impurities exist in very low concentrations. To compute the properties of such defects from first principles (using, e.g., density functional theory), it is common to create a supercell encompassing a few ten to a few hundred atoms, and apply periodic boundary conditions to it. This allows us to use the highly reliable computer codes available for crystalline materials, but amounts to considering a periodic array of defects rather than an isolated one. In principle, by increasing the size of the supercell, the results will converge to that of a single defect. In practice, defect-defect interactions must be expected for those system sizes that can be practically computed.
Correcting for these finite-size effects continues to be a topic until today. One appealing method is to compute a series of supercells, plot the results as function of inverse supercell size (often the length L) and extrapolate to 1/L → 0 assuming a physically motivated function. For instance, isotropic Coulomb interactions decay asymptotically as 1/L. Yet, if the dominant interactions are not clear, or if competing effects are at play, such extrapolations can be misleading. We have looked at two characteristic examples: defect wave function overlap, that decay exponentially, and electrostatic interactions in non-homogeneous environments, notably in slab calculations used for surfaces and 2D materials.
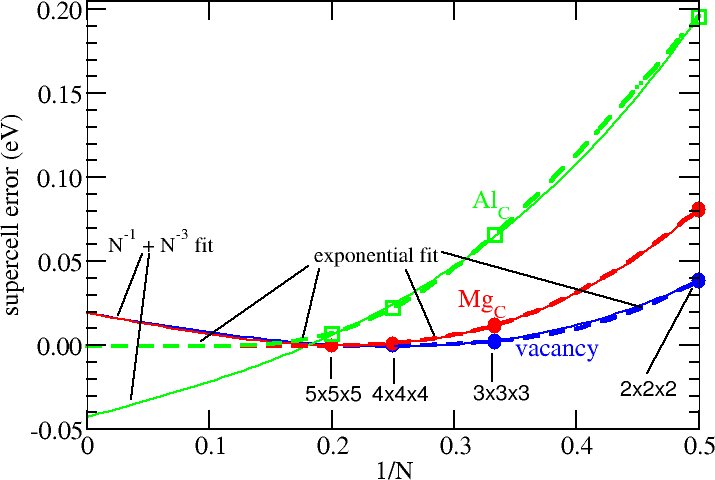
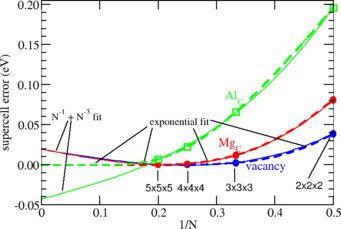
Fig.1 shows one such example for charge-neutral, unrelaxed carbon defects computed in N×N×N supercells. The dominant effect here is wave function overlap, and indeed the energies converge approximately exponentially with increasing supercell size. When empirically extrapolated using a Coulomb-inspired 1/N and an additional 1/N3 term (the scaling of elastic interactions, quadrupole/monopole, dipole-dipole, and other volume-dependent effects), the fits look very very good, but extrapolate to the wrong values when compared with the physically correct exponential model. While this does not really come as a surprise in the present case, wave-function overlap effects may always be present. Even if other Coulomb effects dominate (which often are well captured by 1/N + 1/N3 fits), the presence of errors with a deviating scaling may deteriorate the results.
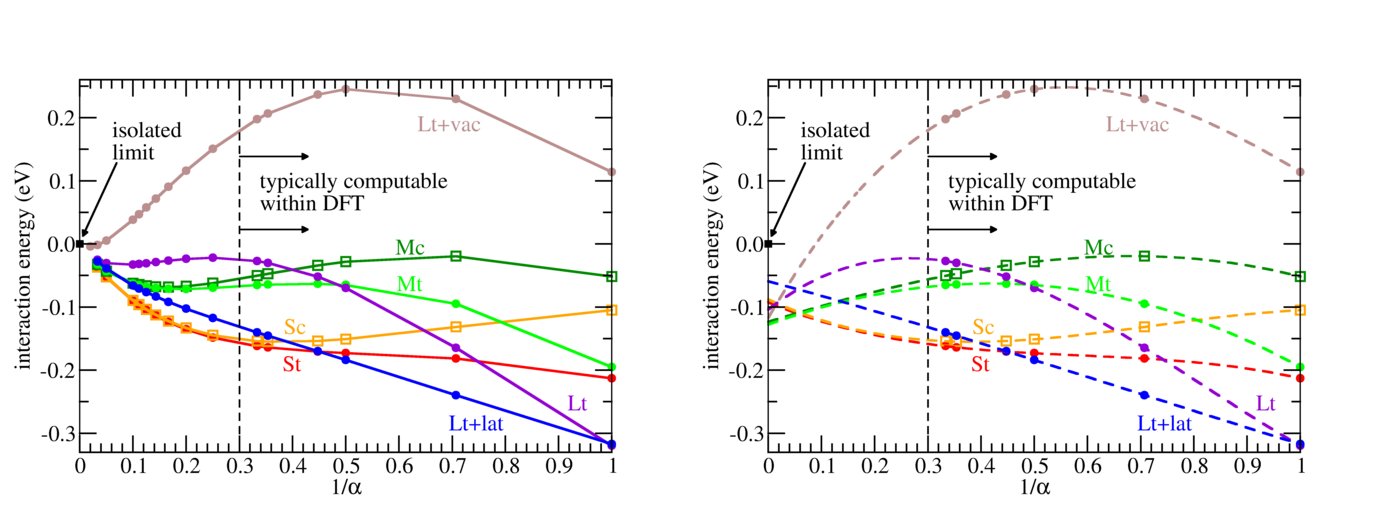
Similar problems occur for electrostatic interactions in inhomogeneous systems. Fig. 2 shows the surprising variability of possible convergence behaviors for a localized charge (with uniform compensating background) located in or near a slab, all computed from a dielectric model. If one uses the small supercells that correspond to cases computable within DFT, and extrapolates to infinite supercell size using a polynomial in the inverse scaling parameter (right image in Fig. 2), one again sees very accurate fits that entirely miss the true behaviour (left image in Fig. 2).
These findings underline the importance of developing correction schemes based on physical understanding rather than relying on empirical schemes, which is one of the long-term activities of our group.