Surface and interface charge corrections
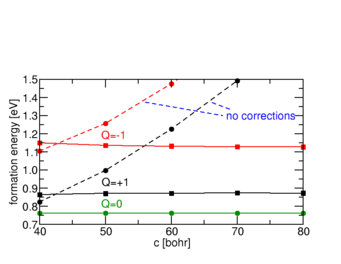
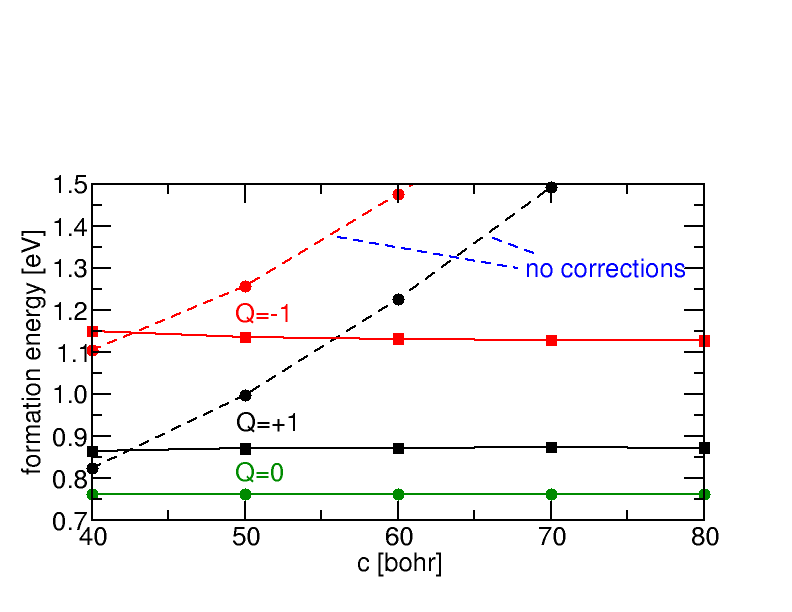
We have extended the sxdefectalign correction scheme to account for charged defects located at surfaces or interfaces. The scheme allows to extrapolate the formation energy of the defect from very small supercells, even if artificial fields in the calculation are sizeable.
Surfaces and interfaces play an enormous role in the function of semiconductor devices such as LEDs, diodes, transistors, etc. Often, the function of the device is directly linked to the properties of the interface. For electrical properties, the charges at or near the surface in addition to macroscopic space charges determine the potential profile at the interface. Point defects are often key sites for the localization of charge right at the interface.
In order to model an interface in detail, however, it is necessary to take into account that defects right at the interface may exhibit modified or even unique properties. Even though the actual structure of the interface is often not known well experimentally, ab initio simulations of idealized surface and interface structures help to identify the key features of real interfaces. An important aspect is the electric behavior of the interface. For instance, the appearance of interface states in the band gap of a semiconductor or insulator will pin the Fermi level at the interface to this state. Electrically active interface defects may play a similar role.
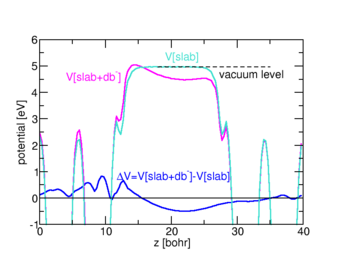
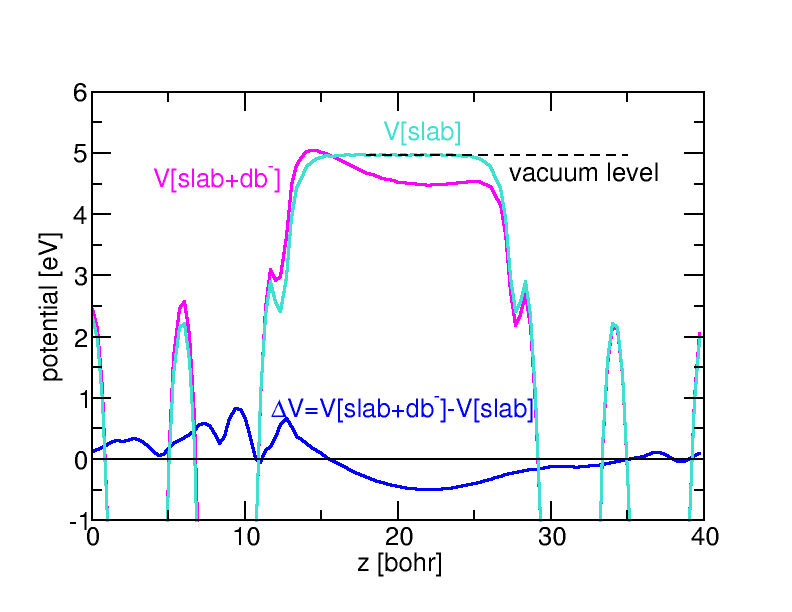
Ab initio calculations can identify the atomistic origin of such defect states by calculating candidate structure in different charge states. The interface is typically modelled as a supercell containing several layers on both sides of the interface, and assuming periodic boundary conditions in all three dimensions. Such ordered structures do not directly yield the energetics of randomly distributed, independent defects of interest, notably in charged states where long-range Coulomb potentials and the necessity to introduce a compensating background result in significant variations between different supercells. To correct for these “artifacts”, we recently developed a correction scheme along the lines of the sxdefectalign correction scheme for bulk defects. The change in screening properties across the interface or surface is modelled by a spatially dependent dielectric constant, which varies as a function of distance from the interface, but is homogeneous in parallel direction. The resulting Poisson equation is solved by the method of image charges generalized to multiple layers, as this allows us to treat both periodic and open boundary conditions on the same footing. By comparing the energy of a charged defect under these two conditions, it is possible to extrapolate the energies of the isolated case already from rather small systems.
The corrections scheme is made available in the form of an executable, sxdefectalign2d. For details, see the add-on download page on the SPHInX homepage.