Optimized key algorithms for our plane-wave DFT code S/PHI/nX

Modern CPUs provide a number of features to increase the computational power. Unfortunately, this increased computing power is often not used in practice, because the CPU can process the data more quickly than the memory can deliver it. To make full use of this enhanced computing power, the existing algorithms need to be revised to better exploit the computing power by exposing hidden parallelism to the CPU and improving the data locality in the data access patterns. We identified key routines in our plane-wave DFT code that offer such tuning opportunities and demonstrate a significant speed-up over standard approaches.

High-performance computing for material science relies on the availability of powerful computer hardware, and computer programs that fully exploit the technical possibilities. Current CPUs use a variety of "tricks" to enhance the execution of programs. Some of these tricks are not specifically aimed at our demands (which consists mostly of floating-point calculations, also called "number crunching"), but might be useful. Others are specifically designed to enhance the throughput for frequent algebraic algorithms. The most important features include (see here very detailed description of what really goes on):

• pipelining - the various stages (decoding of machine code, fetching data from memory, numerical operations, saving data to memory, etc) are run in parallel. While the first machine instruction is executed, the data for the next one may already be loaded from memory, and the third one could be decoded, etc). Moreover, even identical operations that require multiple CPU cycles (e.g. a floating-point operation typically requires 5 cycles) can be pipelined inside the floating-point unit, such that the second multiplication is started while the first one is still running. In consequence, a long sequence of similar operations can be executed with about 1 instruction per cycle. Dissimilar operations, e.g. a floating-point multiplication and an integer addition can even be run independently, increasing the number of instructions per cycle to more than one.
• out-of-order execution - when the pipeline of decoded instructions is long enough, the CPU may execute instructions in a different order than given in the machine code, if the semantics of the code is unchanged. For instance, if there is a long sequence of floating point instructions, with a single integer operation, the integer unit on the CPU is free long before the preceding floating point operations are scheduled. By executing the integer operation early on (provided that it does not interfere with the floating point operations), the result of that instruction is available at an earlier time. A typical situation where this is useful is computations on a vector of numbers, where the memory location of the next data must be computed. By computing and potentially loading the next data before the current computation is finished, the next step may start earlier, speeding up the overall throughput
• speculative branching - if the program flow depends on the outcome of a calculation (e.g. in a loop, where the code must check at each step if the loop is finished), the CPU may continue executing instructions from both possible outcomes of the computation, and then cancel/ignore the outcome of the "wrong" branch.
• register mapping - machine code may use a few dozen "registers" to store and manipulate data directly on the CPU. Modern CPUs translate these machine code registers to a larger number of "internal registers", that are dynamically mapped to the needs of the scheduler. This allows to parallelize operations that semantically require a strict order (e.g. when new data should be loaded into a register that is still needed for a operation waiting to be scheduled). By just "renaming" the internal registers, "future" values of a "machine code register" can already be loaded/computed into a different internal register and renamed once the old value is no longer needed.
• level caches - each CPU core has a one or more small and fast memory ("level caches") attached to it. The level caches replicate the main memory. Memory locations addressed by the CPU that can be found in a cache are then handled by the cache memory in a much faster way. For instance, loading from the level 1 cache (32 KB)  takes 3 cycles, from the level 2 cache (256 KB) takes 11 cycles, and from the main memory ~300 cycles.
• single instruction multiple data (SIMD) - some registers can hold 2 (SSE) or 4 (AVX) double-precision numbers. The mathematical operations on these registers act on all the contained numbers, increasing the throughput per instruction to 2 (SSE) or 4 (AVX)
• fused multiply-add - it is possible to combine a floating-point multiplication and an addition into a single instruction, effectively doubling the number of floating-point operations per instruction. Such combinations frequently appear in algebraic operations.

In consequence, for efficient computations the data processing must be organized algorithmicly such that (a) computations on the same data are combined as much as possible to avoid the memory loading bottleneck, (b) data is organized and processed in vectorizable form. For standard algebraic operations (basic linear algebra subroutines=BLAS and linear algebra package=LAPACK) and fast Fourier transforms, specialized libraries exist that use techniques like blocking, loop unrolling, software pipelining, cache-oblivious divide-and-conquer, etc. to achieve this goal. The performance of these libraries is tremendous - matrix-matrix multiplication for instance can run at incredible 80-90% of the theoretical peak performance (assuming that all instructions are fused-multiply-add of the maximum vector registers of the CPU). FFTs run at 25-50% of the theoretical peak performance. It has therefore been a long-standing strategy in SPHInX to make maximum use of these libraries.

Yet, with the advent of massively parallel hardware such as graphics processors (general-purpose GPUs), we reinvestigated the opportunities to improve the performance our algorithms. The main driving force is that the use of GPUs does not pay off for the presently used library calls, since the data transfer time to the GPU is a significant fraction of the computation time on the CPU. Hence, even if the computation is faster by a factor 10 on the GPU for some portions of the code, the speed-up in the run-time is marginal. The only way out is to combine more operations, to reduce the weight of the data-transfer times. The algorithm design then revealed that even CPU code could be sped up by a significant amount.

Reciprocal space projections onto atom-centered functions

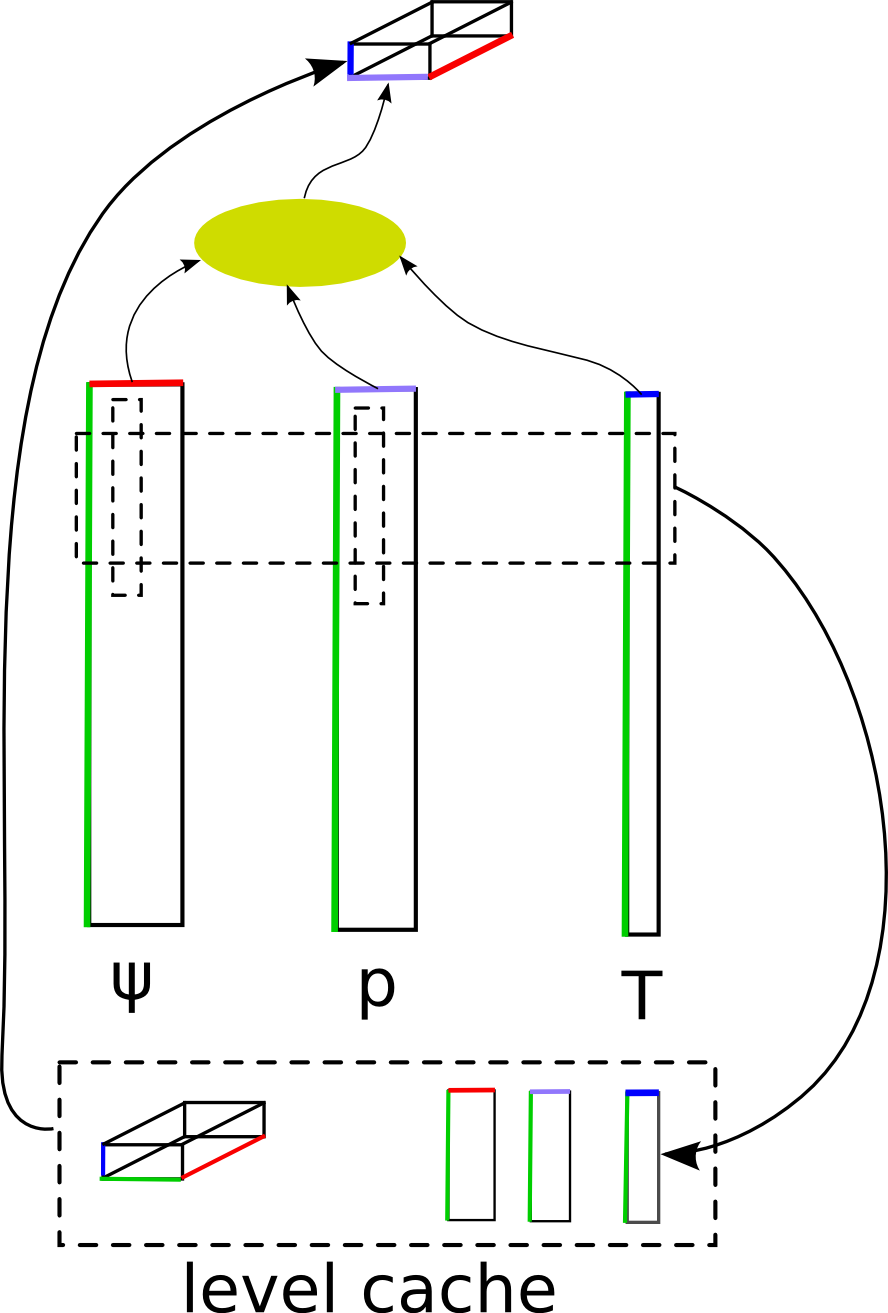
An important fraction of the computational effort in plane-wave computations is the projection onto atom-centered projector functions. While efficient real-space implementations exist, the unavoidable loss in accuracy is often not acceptable for our highly precise calculations. Moreover, we have since long been using a fully blocked reciprocal space algorithm, we were able to rewrite the problem into matrix-matrix multiplication, that is efficiently performed by the BLAS library. This algorithm is faster than the best real-space algorithm for systems with less than 100 atoms.

In reciprocal space, the task is to multiply a complex wavefunction (a vector of plane-wave coefficients), a real projector function (also a vector of plane-wave coefficients), and a complex phase factor to describe the position of the atom (also a vector of plane-wave coefficients), and sum over the plane-wave coefficients to yield a single complex number. This must be done for a several wavefunctions (N_ψ, typically 10-100), several projector functions per atom (N_p, typicaly 10-20), and several atoms (N_a, typically a few 10 to a few 100). The number of plane-wave coefficients (N_G) is much larger (a few 1000 to several 10000). This task is ideally suited for high-performance optimization, because the number of operations (N_ψN_pN_aN_G) is much larger than the data ((N_ψ+N_p+N_a)N_G + N_ψN_pN_a).

Our previous BLAS-based algorithm (basically writing the projector phase-factor product into memory, and the multiplication and G summation as matrix-matrix multiplication) runs at high efficiency, but cannot exploit the fact that the projector functions are real. We have therefore designed a completely new, direct algorithm. In the new algorithm, a small block (several plane-wave coefficients, few wave functions, few atoms) of the two complex vectors are first multiplied into the level 1 cache, and then contracted with the real projectors using a SIMD-vectorized, ψ-block-unrolled algorithm. The inner loop runs at an efficiency close to the theoretical peak performance, overall an efficiency of 50-80% of the theoretical peak performance is achieved in tests, comparable to the best matrix-matrix implementations. The speedup compared to the BLAS algorithm is therefore almost a factor two. Moreover, limited use of higher-level caches makes shared-memory parallelization very efficient.

Direct convolution

Another important step is FFT-based convolutions. In essence, a wave function must be Fourier-transformed in 3 dimensions, multiplied with a real function (in our case: the local potential), and Fourier-transformed back. Due to the sampling theorem, the Fourier mesh must be twice as large in each dimension than the number of non-zero coefficients. Hence, a hypothetical speed-up of a factor 2 could be obtained if it was possible to omit 1D partial Fourier-transforms on rows that are known to contain only zero (or ignored) coefficients. In practice, high-performance FFT libraries intermixes the 1D partial transforms in order to exploit the level caches as an essential technique to achieve high efficiency. Therefore, this hypothetical opportunity was not accessible in practice.

In our new direct convolution algorithm, we overcome this limitation. The key insight is that instead of intermixing the 3D Fourier transforms, we can intermix the forward and backward Fourier transforms as a key to high performance. The multiplication with the potential is then done piecewise on 1D stripes of the Fourier mesh that have just been Fourier transformed and fit into the level 1 cache, and the backward FFT is done directly afterwards. The backward FFT is significantly faster when all data is already in the level 1 cache. The speedup in the innermost loop is then sufficient to compensate for the significantly slower FFT for the first two dimensions. Overall, the speed of the 2D+(1D+multiply+1D)+2D algorithm for the full mesh is roughly as fast as the conventional 3D + multiply + 3D scheme. However, we can now restrict the 2D transforms to the non-zero planes of the full FFT mesh, giving a speedup of a factor two for the full algorithm.