1. Introduction
1.1 Crystalline anisotropy and the spirit of the crystal plasticity finite-element method
The elastic–plastic deformation of crystalline aggregates depends on the direction of loading, i.e. crystals are mechanically anisotropic. This phenomenon is due to the anisotropy of the elastic tensor and to the orientation dependence of the activation of the crystallographic deformation mechanisms (dislocations, twins, martensitic transformations). A consequence of crystalline anisotropy is that the associated mechanical phenomena such as shape change, crystallographic texture, strength, strain hardening, deformationinduced surface roughening, and damage are also orientation dependent. This is not a trivial statement as it implies that mechanical parameters of crystalline matter are tensor quantities.
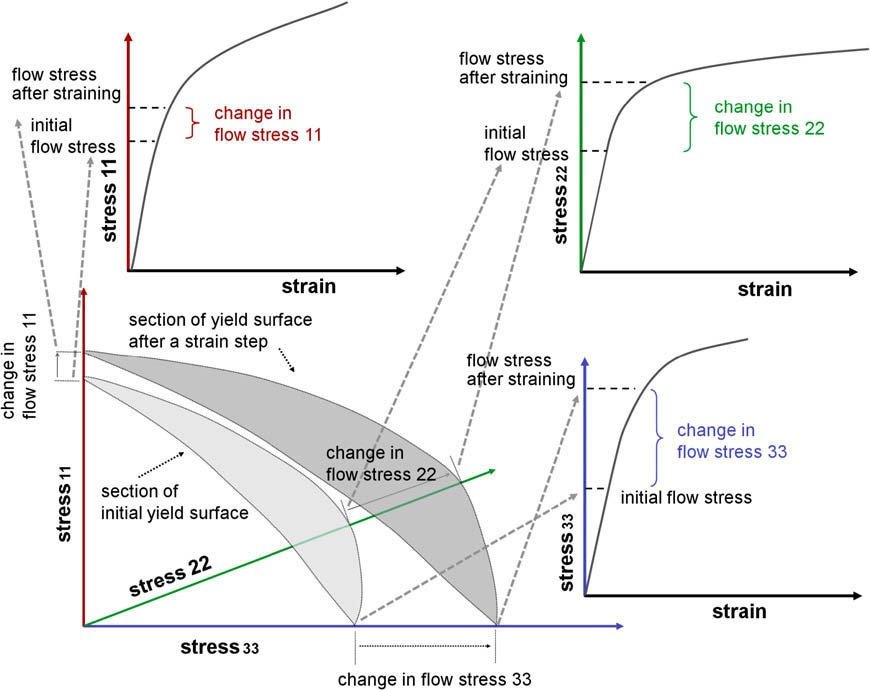
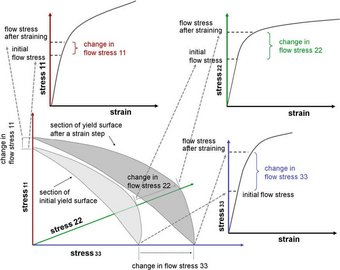
Figure 1: Flow stress and strain hardening of anisotropic materials are tensor quantities.
An example is the uniaxial stress–strain curve, which is the most important mechanical measure in structural materials design. The statement above means that such flow curves represent an incomplete description of plastic deformation as they reduce a 6-dimensional yield surface and its change upon loading to a 1-dimensional (scalar) yield curve, figure 1. Another consequence of this statement is that the crystallographic texture (orientation distribution) and its evolution during forming is a quantity that is inherently connected with plasticity theory. Texture can, hence, be used to describe the integral anisotropy of polycrystals in terms of the individual tensorial behavior of each grain and the orientation dependent boundary conditions among the crystals. Formally, the connection between shear and texture evolution becomes clear from the fact that any deformation gradient can be expressed as the combination of its skew-symmetric portion, which represents a pure rotation leading to texture changes if not matched by the rotation implied by plastic shear, and a symmetric tensor that is a measure of pure stretching. Plastic shear hence creates both shape and orientation changes, except for certain highly symmetric shears. Therefore, a theory of the mechanical properties of crystals must include, first, the crystallographic and anisotropic nature of those mechanisms that create shear, and second, the orientation(s) of the crystal(s) studied relative to the applied boundary conditions (e.g. loading axis, rolling plane).
Early approaches to describe anisotropic plasticity under simple boundary conditions have considered these aspects, such as for instance the Sachs [3], Taylor [4], Bishop–Hill [5, 6], or Kröner [7] formulations. However, these approaches were neither designed for considering explicitly the mechanical interactions among the crystals in a polycrystal nor for responding to complex internal or external boundary conditions, figure 2. Instead, they are built on certain simplifying assumptions of strain or stress homogeneity to cope with the intricate interactions within a polycrystal.
![Figure 2: Schematical presentation of the growing complexity of grain-scale mechanics with respect to the equilibrium of the forces and the compatibility of
the displacements for different situations. (a and b) Single slip problem in a single crystal presented in stress space. (c) Part of a single-crystal yield surfacewith two slip systems. (d) Multislip situation in a polycrystal where all different crystals have to satisfy an assumed imposed strain in their respective yieldcorners. If the strain is homogeneous, this situation leads to different stresses in each crystal [1,2]. scrit : critical shear stress. τcrit: critical shear stress. σTBH : Taylor-Bishop-Hill stress state (stress required to reach a yield corner).](/3747963/original-1518437998.jpg?t=eyJ3aWR0aCI6OTY2LCJvYmpfaWQiOjM3NDc5NjN9--c577be50c54d31fc3b8ea325cd1cf54003389621)
For that reason variational methods in the form of finite element approximations have gained enormous momentum in this field. These methods, which are referred to as crystal plasticity finite element (CPFE) models, are based on the variational solution of the equilibrium of the forces and the compatibility of the displacements using a weak form of the principle of virtual work in a given finite volume element. The entire sample volume under consideration is discretized into such elements. The essential step which renders the deformation kinematics of this approach a crystal plasticity formulation is the fact that the velocity gradient is written in dyadic form. This reflects the tensorial crystallographic nature of the underlying defects that lead to shear and consequently, to both shape changes (symmetric part) and lattice rotations (skew-symmetric part), see section 3. This means that the CPFE method has evolved as an attempt to employ some of the extensive knowledge gained from experimental and theoretical studies of single crystal deformation and dislocations to inform the further development of continuum field theories of deformation. The general framework supplied by variational crystal plasticity formulations provides an attractive vehicle for developing a comprehensive theory of plasticity that incorporates existing knowledge of the physics of deformation processes [8, 9, 10] into the computational tools of continuum mechanics [11, 12] with the aim to develop advanced and physically based design methods for engineering applications [13].
![Figure 3: Experimental example of the heterogeneity of plastic deformation at the grain and sub-grain scale using an aluminum polycrystal with large columnar grains [14]. The images show the distribution of the accumulated von Mises equivalent strain in a specimen after 8 % and 15 % plane strain sample thickness reduction (the deformation is given in % of Δ d/d, where d is the sample extension along compression direction). The experiment was conducted in a lubricated channel-die set-up. The strains were determined using digital image correlation. The high angle grain boundaries indicated by white lines were taken from EBSD microtexture measurements. The equivalent strains differ across some of the grain boundaries by a factor of 4–5 giving evidence of the enormous orientation-dependent heterogeneity of plasticity even in pure metals.](/3747952/original-1518437997.jpg?t=eyJ3aWR0aCI6OTY2LCJvYmpfaWQiOjM3NDc5NTJ9--f22fbdc5fb77cee9616969e71865e22bd1863bd3)
Figure 3: Experimental example of the heterogeneity of plastic deformation at the grain and sub-grain scale using an aluminum polycrystal with large columnar grains [14]. The images show the distribution of the accumulated von Mises equivalent strain in a specimen after 8 % and 15 % plane strain sample thickness reduction (the deformation is given in % of Δ d/d, where d is the sample extension along compression direction). The experiment was conducted in a lubricated channel-die set-up. The strains were determined using digital image correlation. The high angle grain boundaries indicated by white lines were taken from EBSD microtexture measurements. The equivalent strains differ across some of the grain boundaries by a factor of 4–5 giving evidence of the enormous orientation-dependent heterogeneity of plasticity even in pure metals.
One main advantage of CPFE models lies in their capability of solving crystal mechanical problems under complicated internal and/or external boundary conditions. This aspect is not a mere computational advantage but it is an inherent part of the physics of crystal mechanics since it enables one to tackle those boundary conditions that are imposed by inter-and intragrain micro-mechanical interactions, figure 3 [14]. This is not only essential to study in-grain or grain cluster mechanical problems but also to better understand the often quite abrupt mechanical transitions at interfaces [15].
However, the success of CPFE methods is not only built on their efficiency in dealing with complicated boundary conditions. They also offer high flexibility with respect to including various constitutive formulations for plastic flow and hardening at the elementary shear system level.
The constitutive flow laws that were suggested during the last decades have gradually developed from empirical viscoplastic formulations [16, 17] into physics-based multiscale internal-variable models of plasticity including a variety of sizedependent effects and interface mechanisms [18, 19, 9, 20, 21, 22, 23, 24, 25, 26]. In this context it should be emphasized that the finite element method itself is not the actual model but the variational solver for the underlying constitutive equations that map the anisotropy of elastic–plastic shears associated with the various types of lattice defects (e.g. dislocations, twins, martensite). Since its first introduction by Peirce, Asaro and Needleman in 1982 [27] the CPFE method has matured into a whole family of constitutive and numerical formulations which has been applied to a broad variety of crystal mechanical problems, table 1.
Table 1
Some examples for different applications of the CPFE method.
| Application of the CPFE method | Reference |
| Surface roughening, ridging, roping, thin film mechanics | Becker [28], Raabe et al. [15], Zhao et al. [29], Yue [30], Siska et al. [31], Zhao et al. [32] |
| Grain boundary mechanics, Hall–Petch behavior, grain interaction, grain size effects, strain gradient effects, non-local formulations, interface mechanics, superplasticity |
Becker and Panchanadeeswaran [33], Mika and Dawson [34], Acharya and Beaudoin [35], Meissonnier et al. [36], Barbe et al. [37], Raabe et al. [38], Evers et al. [20], Park et al. [39], Clarke et al. [40], Wei and Anand [41], Fu et al. [42], Evers et al. [26], Evers et al. [21], Diard et al. [43], Bate and Hutchinson [44], Wei et al. [45], Murphy et al. [46], Deka et al. [47], Ma et al. [24], Ma et al. [25], Counts et al. [48], Gurtin et al. [49], Venkatramani et al. [50], Okumura et al. [51], Gerken and Dawson [52], Gerken and Dawson [53], Kuroda and Tvergaard [54], Bitzek et al. [55], Borg et al. [56], Li et al. [57] |
| Creep, high temperature deformation, diffusion mechanisms |
McHugh and Mohrmann [58], Balasubramanian and Anand [59], Hasija et al. [60], Bower and Wininger [61], Venkatramani et al. [50], Agarwal et al. [62], Venkataramani et al. [63], Xu et al. [64] |
| Dislocation-based constitutive modeling | Arsenlis and Parks [18], Arsenlis and Parks [19], Arsenlis and Tang [65], Arsenlis et al. [9], Evers et al. [20], Evers et al. [21], Cheong and Busso [22], Ma and Roters [23], Evers et al. [26], Ma et al. [24], Ma et al. [25], McDowell [66], Li et al. [57] |
| Martensite mechanics, phase transformation, shape memory |
Marketz and Fischer [67], Marketz and Fischer [68], Tomita and Iwamoto [69], Diani et al. [70], Diani and Parks [71], Cherkaoui et al. [72], Cherkaoui et al. [73], Thamburaja and Anand [74], Tomita and Iwamoto [75], Govindjee and Miehe [76], Anand and Gurtin [77], Turteltaub and Suiker [78], Thamburaja [79], Lan et al. [80], Turteltaub and Suiker [81], Tjahjanto et al. [82], Geers and Kouznetsova [83] |
| In-grain texture, grain-scale mechanics, mesoscale, non-uniform deformation |
Peirce et al. [27], Peirce et al. [84], Beaudoin et al. [85], Mika and Dawson [34], Sarma and Dawson [86], Sarma and Dawson [87], Sarma et al. [88], Forest [89], Bhattacharyya et al. [90], Raabe et al. [38], Miller and Turner [91], Raabe et al. [92], Sachtleber et al. [14], Kim and Oh [93], Clarke et al. [40], Choi [94], Zaefferer et al. [95], Erieau and Rey [96], Sarma and Radhakrishnan [97], Roters et al. [98], Kim et al. [99], Murphy et al. [46], daFonseca et al. [100], You et al. [101], Musienko et al. [102], Han and Dawson [103], Zhao et al. [32], Zhang et al. [104] |
| Texture evolution, texture stability, in-grain texture formation, anisotropy | Asaro and Needleman [105], Becker [106], Becker et al. [107], Bronkhorst et al. [108], Kalidindi et al. [109], Beaudoin et al. [110], Bertram et al. [111], Becker and Panchanadeeswaran [33], Beaudoin et al. [110], Mika and Dawson [112], Miehe et al. [113], Kalidindi [114], Balasubramanian and Anand [59], Van Houtte et al. [115], Delannay et al. [116], Raabe et al. [117], Bate and An [118], Raabe et al. [119], Li et al. [120], Sarma and Radhakrishnan [97], Anand [121], Roters et al. [122], Van Houtte et al. [123], Li et al. [124], Van Houtte et al. [125], Delannay et al. [126], Tang et al. [127], Tikhovskiy et al. [128], Lee et al. [129], Tikhovskiy et al. [130], Mayeur et al. [131], Delannay et al. [132] |
| Forming, deep drawing, process modeling, cup drawing, spring-back, earing, wire drawing, extrusion, anisotropy, design, fretting | Beaudoin et al. [133], Beaudoin et al. [134], Neale [135], Kalidindi and Schoenfeld [136], Nakamachi et al. [137], Zhao et al. [138], Xie and Nakamachi [139], Raabe et al. [1] Goh et al. [140], McGarry et al. [141], Raabe and Roters [142], Zhao et al. [13], Tugcu et al. [143], Delannay et al. [144], Li et al. [124], Raabe et al. [145], Dick and Cailletaud [146], Tikhovskiy et al. [128], Delannay et al. [126], Chen et al. [147], Raabe [148], Nakamachi et al. [149], Ocenasek et al. [150], Tikhovskiy et al. [130], Mayeur et al. [131], Li et al. [151], Li et al. [152], Zhuang et al. [153], Delannay et al. [132], Zamiri et al. [154] |
| Crystal plasticity and recrystallization | Bate [155], Raabe and Becker [156], Raabe [157], Radhakrishnan et al. [158], Raabe [159], Takaki et al. [160], Raabe [148], Semiatin et al. [161], Zambaldi et al. [162], Loge et al. [163] |
| Deformation twinning | Kalidindi [164], Staroselsky and Anand [165], Marketz et al. [166], Staroselskya and Anand [167], Marketz et al. [168], Salem et al. [169] |
| Nanoindentation, pillar testing, micro-bending, micro-scale deformation and testing |
Wang et al. [170], Zaafarani et al. [171], You et al. [101], Raabe et al. [172], Casals et al. [173], Zaafarani et al. [174], Alcala et al. [175], Weber et al. [176], Xu et al. [64], Demir et al. [177] |
| Numerical aspects, FE shape effects, mesh dependence, accuracy, robust integration methods, texture discretization |
Miehe [178], Bachu and Kalidindi [179], Harewood and McHugh [180], Amirkhizi and Nemat-Nasser [181], Harewood and McHugh [182], Kuchnicki et al. [183], Melchior and Delannay [184], Zhao et al. [185], Li et al. [186], Ritz and Dawson [187], Barton et al. [188], Gerken and Dawson [52] |
| Damage, fatigue, cyclic loading, void growth | Bruzzi et al. [189], Turkmen et al. [190], Turkmen et al. [191], Kysar et al. [192], Sinha and Ghosh [193], Potirniche et al. [194], Zhang et al. [195], Cheong et al. [196], Dunne et al. [197], Liu et al. [198], Bieler et al. [199], Kumar et al. [200], Patil et al. [201], Watanabe et al. [202], McDowell [66], Mayama et al. [203], Borg et al. [56] |
| Multiphase mechanics | Hartig and Mecking [204], Tjahjanto et al. [205], Mayeur et al. [131], Inal et al. [206], Vogler and Clayton [207] |
1.2. The crystal plasticity finite-element method as amultimechanism and multiphysics platform
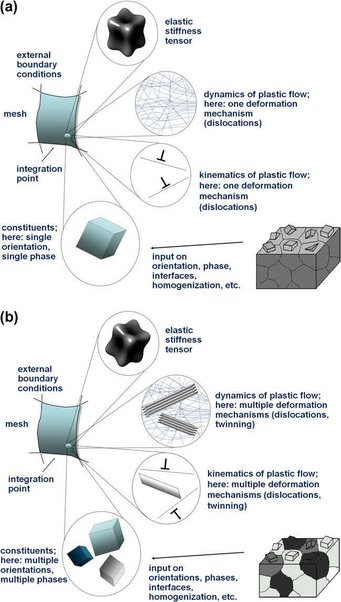
A conceptual advantage of the CPFE approach is that it may not only include dislocations but also other mechanisms which follow dyadic kinematics such as martensite formation [74,80], shear band formation (e.g. in glassy matter) [208,209], mechanical twinning [164–166,169] and even superplastic grain boundary shear [41,45]. The CPFE method allows the user to implement these shear mechanisms including their interactions. But it also adds complexity to the model: the use of different competing crystallographic deformation mechanisms within a CPFE model requires the formulation of local homogenization rules [1,142]. This means that at some material points only one type of deformation mechanism (e.g. dislocation slip) may occur, while in others a mix (e.g. dislocations and twins) must be considered within the same volume portion. The latter situation requires appropriate submodels that describe the evolving fractions (e.g. of the twinned volume) and the interactions of coexisting and competing deformation mechanisms at the same field point (Fig. 4). An aspect that increases complexity in such cases is the possibility that deformation martensite or twins may, after their formation, undergo further plastic deformation or create accommodation strains related to volume changes. Some of these aspects will be discussed in Sections 5 and 6.
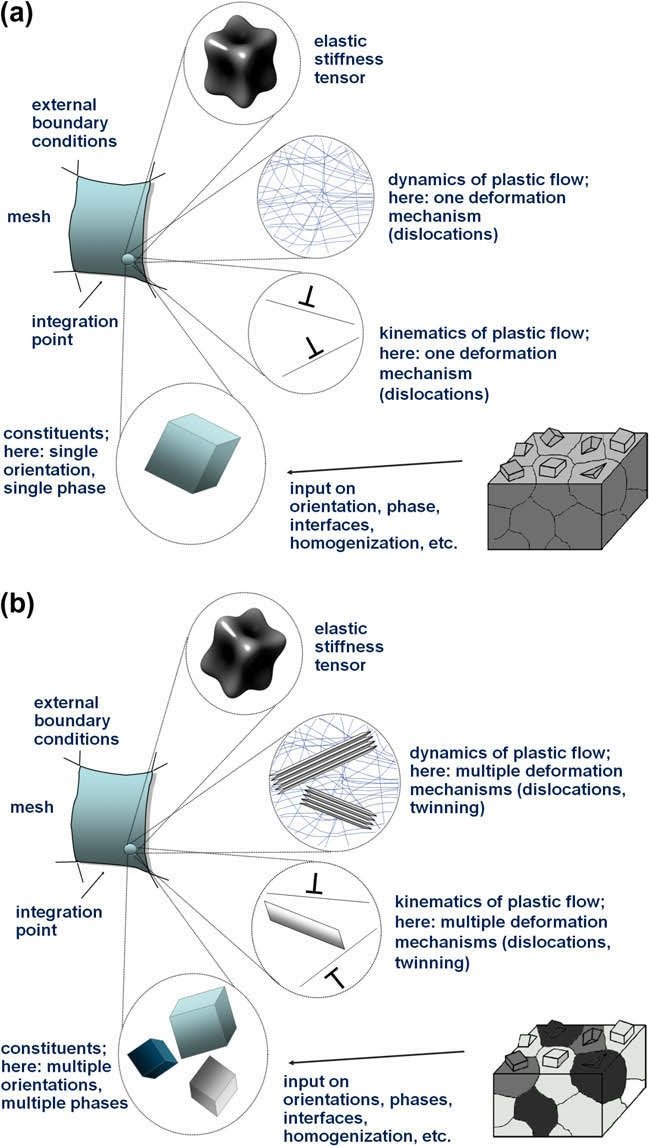
Another strength of the CPFE method is the close connection between shape change, rotation and geometrically necessary dislocations (GNDs) [210–213]. This allows one to implement constitutive laws that treat mechanical size effects in conjunction with local orientation gradients [24]. This point is relevant for size-dependent plasticity modeling, as the polarized portions of dislocation arrays (which are often conceptually treated as GNDs),1 such as anticipated in many size effect models, must necessarily coincide with orientation gradients [210]. Such lattice rotations are nowadays accessible to precise and high-resolution measurements in 2-D and 3-D so that corresponding models can be tested [95,98,171,177,214–216].
CPFE simulations can be used both at microscopic and macroscopic scales [1]. Examples for small-scale applications are inter- and intra-grain mechanics, damage initiation, mechanics at interfaces, simulation of micromechanical experiments (e.g. indentation, pillar compression, beam bending), or the prediction of local lattice curvatures and mechanical size effects (see Table 1). Consequently, CPFE methods gain momentum for the field of small-scale material testing where the experimental boundary conditions are difficult to control and/or monitor. In such cases the experimental results may sometimes be hard to interpret without corresponding CPFE simulations that allow an experimentalist to simulate the effects of details in the contact and boundary conditions. Miniaturization also occurs in engineering design. Many products nowadays have dimensions in the range of the grain scale, e.g. microelectromechanical systems (MEMS), bonding wires and pillars, stents, and practically all materials in electronic components. Design of such parts increasingly requires consideration of grain-scale crystalline anisotropy. Some applications along these lines are discussed in Section 9.
1It should be noted that a dislocation does actually not know whether it is a geometrically necessary one or a statistical one unless its state is specified in the context of an adequately defined Frank loop around a material portion of interest. Also then geometrically necessary dislocations are from a physics standpoint not a separate type of lattice defect when compared to statistically stored dislocations, i.e. their evolution must be embedded in a unified kinetic framework so that they can assume either state depending on the local lattice defect configuration.
Macroscopic applications of the CPFE method occur particularly in the fields of large-scale forming and texture simulations. These problems usually require appropriate homogenization schemes within a CPFE model since a larger number of crystals and/or phases must be considered in each representative volume element mapped at a FE integration point. Primary engineering objectives of CPFE applications in macroscopic forming simulations are the prediction of the precise material shape after forming, thickness distribution, material failure, optimization of material flow, elastic spring-back, forming limits, texture evolution and the mechanical properties of the formed part [13,137–139,145,217]. Further related applications occur in tool design, press layout and surface properties (see references in Table 1). The latter aspect involves both macroscopic (e.g. wrinkling) as well as microstructural (e.g. roping, ridging, orange peel) mechanisms that influence the surface topography [15,28,29]. A recent development is the use of the CPFE method as a virtual mechanical laboratory. This approach uses crystal plasticity simulations instead of complicated mechanical tests that are required for fitting yield surface coefficients [217].
A further advantage of CPFE predictions is that they can be compared to experiments in a very detailed fashion probing a variety of quantities (Table 2). Corresponding studies compared shape changes, forces, strains, strain paths, rate effects, texture evolution, interface response, local stresses and size effects one-to-one at different scales (Table 2). Examples for applications and experimental validation procedures are given in Section 9.
Table 2: Examples of measurable quantities that can be predicted by CPFE models
Prediction by CPFE methods and Experimental access:
| Surface roughening | Speckle interferometry, digital image correlation (photogrammetry), atomic force microscopy, white-light confocal microscopy |
| Elasticity, interface mechanics, grain size effects, grain interaction, size effects | Indentation testing, tensile and compression testing, mechanical tests at different sample sizes, digital image correlation, electron backscatter diffraction, scanning electron microscopy, ultrasonic testing, x-ray and synchrotron Bragg peak broadening and shifting |
| Creep, high temperature deformation, superplasticity | tensile testing, texture measurement, in-situ electron microscopy |
| Dislocation-based constitutive modeling | Flow stress measurement, transmission electron microscopy, lattice orientation measurements, electron channeling contrast imaging in the scanning electron microscope |
| Martensite mechanics, phase transformation, shape memory | Magnetic measurements, multiphase electron backscatter diffraction, x-ray and synchrotron Bragg diffraction |
| In-grain texture, grain-scale mechanics, non-uniform deforma tion, multiphase mechanics | Digital image correlation, indentation hardness testing, orientation determination (Kikuchi diffraction in the transmission or scanning electron microscope; x-ray Bragg diffraction), mechanical testing |
| Texture evolution, texture stability, in-grain texture formation, anisotropy | Texture measurements using Kikuchi diffraction in the transmission and scanning electron microscope or x-ray Bragg diffraction |
| Forming, deep drawing, process modeling, cup drawing, spring back, earing, wire drawing, extrusion, anisotropy, design, fretting Prediction by CPFE methods Crystal plasticity and recrystallization | Hardness testing, metallography, electrical resistivity, x-ray and synchrotron diffraction, electron backscatter diffraction, transmission electron microscopy, grain size determination, kernel average orientation determination, calorimetry |
| Deformation twinning | Metallography, x-ray and synchrotron diffraction, electron backscatter diffraction, transmission electron microscopy, electron channeling contrast imaging in the scanning electron microscope |
| Nanoindentation, micro-scale deformation, miniaturized mechanical testing |
Hardness and stiffness analysis using nanoindenter or nano-manipulator tests, surface shape analysis using atomic force microscopy, electron microscopy |
Beyond these metallurgical and mechanical considerations numerical aspects also deserve attention. CPFE formulations can be either fully integrated into FE codes or implemented as user-defined subroutines into commercially available solvers. The latter point is important because engineering applications are often tackled using commercial platforms. The use of standard solvers also helps to make CPFE methods accessible to a broader community. Since details of the FE method, the mesh and the integration procedures also play a significant role in CPFE simulations, some of these aspects are discussed in Section 8.
In summary, this review intends to demonstrate that for micro- and macro-scale mechanical problems containing dyadic degrees of freedom for shear, the CPFE method is an effective modeling platform as it can deal with the delicate interplay of different effects such as complicated boundary conditions (e.g. imposed by the surrounding microstructure or by external fields), various deformation mechanisms and their interactions (e.g. dislocation mechanics at interfaces or twins and martensite), interface properties (e.g. structural superplasticity or the Hall–Petch effect) and details of slip localization (e.g. shear band formation) at reasonable computational costs and by using open source or commercial solvers.
![Figure 2: Schematical presentation of the growing complexity of grain-scale mechanics with respect to the equilibrium of the forces and the compatibility of
the displacements for different situations. (a and b) Single slip problem in a single crystal presented in stress space. (c) Part of a single-crystal yield surfacewith two slip systems. (d) Multislip situation in a polycrystal where all different crystals have to satisfy an assumed imposed strain in their respective yieldcorners. If the strain is homogeneous, this situation leads to different stresses in each crystal [1,2]. scrit : critical shear stress. τcrit: critical shear stress. σTBH : Taylor-Bishop-Hill stress state (stress required to reach a yield corner). Figure 2: Schematical presentation of the growing complexity of grain-scale mechanics with respect to the equilibrium of the forces and the compatibility of
the displacements for different situations. (a and b) Single slip problem in a single crystal presented in stress space. (c) Part of a single-crystal yield surfacewith two slip systems. (d) Multislip situation in a polycrystal where all different crystals have to satisfy an assumed imposed strain in their respective yieldcorners. If the strain is homogeneous, this situation leads to different stresses in each crystal [1,2]. scrit : critical shear stress. τcrit: critical shear stress. σTBH : Taylor-Bishop-Hill stress state (stress required to reach a yield corner).](/3747963/original-1518437998.jpg?t=eyJ3aWR0aCI6MzQxLCJmaWxlX2V4dGVuc2lvbiI6ImpwZyIsIm9ial9pZCI6Mzc0Nzk2M30%3D--9fcb7f460e6f94ffaaf5f52a6e3874062de05f1a)
![Figure 3: Experimental example of the heterogeneity of plastic deformation at the grain and sub-grain scale using an aluminum polycrystal with large columnar grains [14]. The images show the distribution of the accumulated von Mises equivalent strain in a specimen after 8 % and 15 % plane strain sample thickness reduction (the deformation is given in % of Δ d/d, where d is the sample extension along compression direction). The experiment was conducted in a lubricated channel-die set-up. The strains were determined using digital image correlation. The high angle grain boundaries indicated by white lines were taken from EBSD microtexture measurements. The equivalent strains differ across some of the grain boundaries by a factor of 4–5 giving evidence of the enormous orientation-dependent heterogeneity of plasticity even in pure metals. Figure 3: Experimental example of the heterogeneity of plastic deformation at the grain and sub-grain scale using an aluminum polycrystal with large columnar grains [14]. The images show the distribution of the accumulated von Mises equivalent strain in a specimen after 8 % and 15 % plane strain sample thickness reduction (the deformation is given in % of Δ d/d, where d is the sample extension along compression direction). The experiment was conducted in a lubricated channel-die set-up. The strains were determined using digital image correlation. The high angle grain boundaries indicated by white lines were taken from EBSD microtexture measurements. The equivalent strains differ across some of the grain boundaries by a factor of 4–5 giving evidence of the enormous orientation-dependent heterogeneity of plasticity even in pure metals.](/3747952/original-1518437997.jpg?t=eyJ3aWR0aCI6MzQxLCJmaWxlX2V4dGVuc2lvbiI6ImpwZyIsIm9ial9pZCI6Mzc0Nzk1Mn0%3D--21dc423f3828636165f663cb033e9abdcab67bf0)