Plastic effects on the kinetics of phase transformations
Many solid state phase transformations e.g. in steels or shape memory alloys are accompanied by severe mechanical deformations during the microstructure evolution. In contrast to elastic effects, which can nowadays be included e.g. in a phase field formulation of these processes, the proper incorporation of plastic deformation is not yet established. The reason is that different dissipative processes play a role here, which influence the motion of the interface. In this project we intend to develop novel sharp interface and phase field methods to simulate the microstructure evolution in the plastic regime.
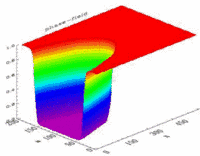
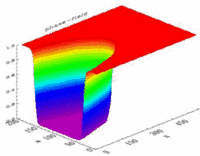
Fig. 1: The order parameter in a phase field model distinguishes between the different phases. At an interface, it changes its value continuously, and in the bulk phases it is spatially constant.
© Robert Spatschek, Max-Planck-Institut für Eisenforschung GmbH

Fig. 2: Simple stress-strain curve involving a phase transformation.
© Robert Spatschek, Max-Planck-Institut für Eisenforschung GmbH
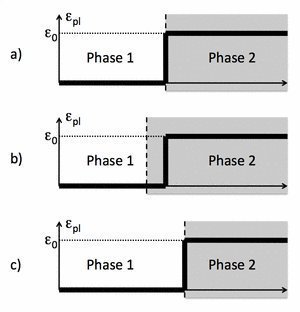
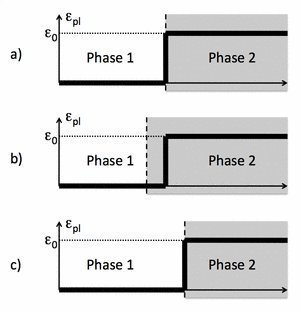
Fig. 3: Asymmetric growth scenario. Starting from configuration (a), where the dashed vertical line depicts the interface between phase 1 and 2, in (b) phase 2 has grown. However, in the newly converted phase the plastic strain is adopted from the mother phase, i.e. the plastic strain is now inhomogeneous in phase 2. For growth in the other direction (c), it is assumed that phase 1 stays in a homogenous plastic strain state.
© Robert Spatschek, Max-Planck-Institut für Eisenforschung GmbH