Mechanism Oriented Steel Development

F. Roters, D. Raabe

This progress report discusses how physically based material models can contribute to the development and optimization of new materials. Using in addition enhanced simulation techniques such as density functional theory a true multi scale material development can be established.

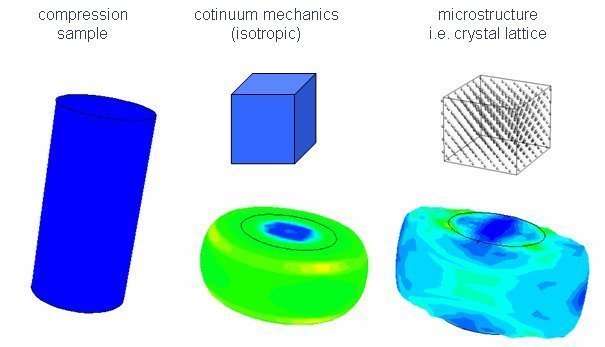
Figure 1: Effect of using a very simple isotropic material law in comparison to a more physical crystal plasticity model.

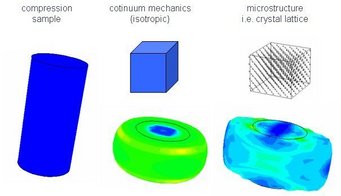
The development of new materials is nowadays strongly correlated with materials simulation. Taking the view of a part manufacturer it is mainly the bulk mechanical properties that are of interest. This is the reason why continuum material models still dominate the field of constitutive models. However, with increasing demands on modeling accuracy the shortcomings of this kind of models become more and more visible and an increasing tendency for the usage of more physical models can be observed. Figure 1 gives a simple example for the comparison of a continuum and a more physical model. While the example is certainly somewhat exaggerated it still illustrates the main point. While one needs to make certain assumptions for the continuum model (isotropy in this case) the more physical crystal plasticity model naturally accounts for the material anisotropy. Nevertheless, the crystal plasticity model still is a homogenized one that only accounts for the geometry of the material deformation by dislocation slip. One, therefore, has to be aware of the fact, that the performance of a lot of new materials is strongly influenced by local processes, e.g. formation of twins or triggering of phase transformations, which are still not included in this kind of models.

The Crystal Plasticity Finite Element Method (CPFEM, [1-6]) takes into account the crystalline nature of most metallic materials. Crystalline materials mainly deform by slip of dislocations on crystallographically predefined slip systems.

References

  1. D. Pierce, R. J.  Asaro, A. Needleman. Acta Metallurgica 1982 30 1087
  2. R. J. Asaro; Advances in Applied Mechanics 1983 23 1
  3. D. Pierce, R. J. Asaro, A. Needleman; Acta Metallurgica 1983 31 1951
  4. A. Needleman,  R. J. Asaro; Acta Metallurgica 1985 33 923
  5. K. K. Mathur, P. R. Dawson; International Journal of Plasticity 1989 5 67
  6. S. R. Kalidindi, C. A. Bronkhorst, L. Anand; Journal on the Mechanics and Physiscs of Solids 1992 40 537
Web-View
Print Page
Open in new window
Estimated DIN-A4 page-width
Go to Editor View