Solidification in syntectic and monotectic alloys
We study steady-state solidification along the liquid-liquid interface in a syntectic system by means of a boundary-integral technique. We study the case of small asymmetry of the pattern and extract from the results the scaling relations in terms of the undercooling and the asymmetry parameter. We also investigate monotectic solidification using the phase-field method.
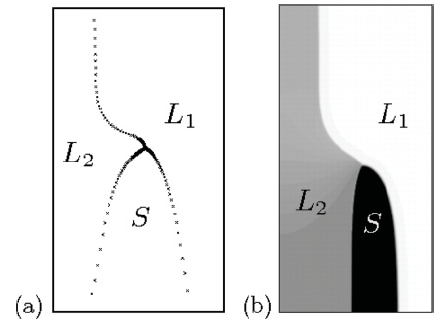
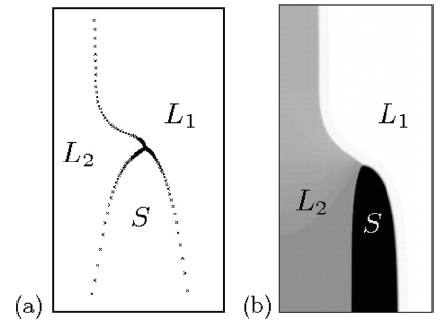
Fig. 1: Steady-state pattern during monotectic solidification, obtained with (a) boundary-integral equations and (b) a phase-field simulation.
© Claas Hüter, Max-Planck-Institut für Eisenforschung GmbH
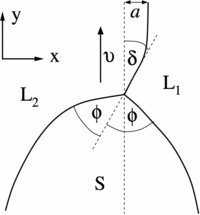
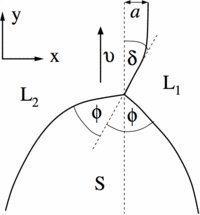
Fig. 2: Close-up of the triple junction region for a typical dendritic front propagation in syntectic systems. The solid S grows with velocity v along the metastable liquid-liquid (L1/L2) interface. In the x direction, the triple junction is shifted by a distance a from the asymptotic position of the liquid-liquid interface. The latter adopts at the triple junction an angle with the velocity direction.
© Claas Hüter, Max-Planck-Institut für Eisenforschung GmbH