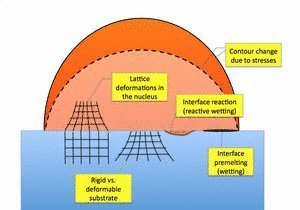
Heterogeneous nucleation is a fascinating and challenging topic already for a long time. Experimental investigations are known to be difficult in metallic systems, and therefore the investigation of colloidal systems is a promising approach to observe these processes for obtaining a deeper understanding. In the framework of classical descriptions nucleation is understood as an energetic competition between a surface and a bulk term. Depending on interfacial energies, heterogeneous nucleation at walls or impurities is often favored in comparison to homogeneous nucleation. This can be understood from a macroscopic relation by Turnbull which links the energy barriers for homogeneous and heterogeneous nucleation by a catalytic potency factor which depends only on the contact angle between the substrate and the adsorbate. This itself is determined by the interfacial energies present at the triple junction. This relation is based on the assumption that the nucleus forms as a spherical cap on the surface, which neglects surface anisotropies. It has recently been verified for a nanoscopic model using an Ising lattice gas model, and it has been pointed out that line tension effects are important and lead to a modification of the Turnbull formula, and in particular negative line tensions have been found.
Newkirk and Turnbull generalized the expression by taking into account lattice mismatch effects, which lead to the appearance of an additional bulk energy term, which is quadratic in the strain mismatch (disregistry). The comparison to experimental results for nucleation of ammonium iodide from aqueous solutions on mica however does not lead to quantitative agreement and the elastic constants have to be assumed to be 1 or 2 orders of magnitude smaller then the theoretical expectation to obtain agreement between theory and experiment. This unsatisfactory finding might be attributed to the fact that the actual elastic problem is not solved but a homogeneous strain distribution is assumed. In reality, however, strong strain relaxation takes place by full elastic equilibration, since the cap of the nucleus is subjected to a hydrostatic stress only.
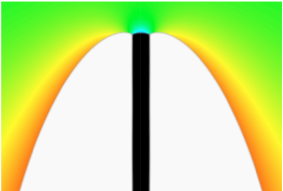
Furthermore, the central condition, the spherical shape of the cap, will most likely be violated by the presence of elastic effects, since they typically induce nonhydrostatic stress states inside the nucleus, and therefore the chemical potential at the top surface, which determines the shape of the cap, is no longer given by curvature effects only. This is also known from heteroepitaxy, where island formation (apart from faceting effects) happens in more complicated structures than spherical caps. This example already shows that the influence of elastic effects on heterogeneous nucleation is - despite their importance - not yet sufficiently understood.
In general, major reasons for the appearance of elastic effects are:
- Lattice mismatches or structural dissimilarities between substrate and nucleus,
- Heterogeneous nucleation on curved substrates, which leads to deformations of the growing phase,
- Defects and grain boundaries,
- Concentration and thermal gradients.