GPU computing
Modern graphics cards offer enormous computational capabilities for scientific computing with minimal costs. We are using this technology for phase field and amplitude equations simulations on a regular basis, with a gain of efficiency by up to a factor 250 in comparison to a single core CPU computation. This tremendous speedup is extremely valuable, as it reduces the time for individual simulations to finish drastically and therefore leads to much shorter development cycles also for new codes and applications to new problems.
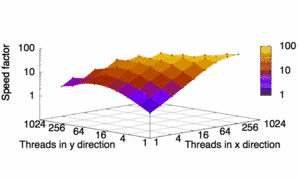
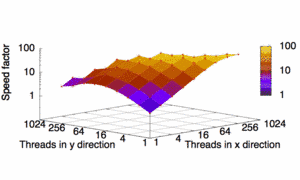
Fig. 1: Phase field simulations on graphics cards demand to find an optimal thread distribution. For the present example of the simulation of phase change materials for nonvolatile data storage we can reach a speed increase up to a factor 100.
© Alexander Monas, Max-Planck-Institut für Eisenforschung GmbH

Fig. 2: Amplitude equations modeling of solidification of delta-iron, performed on graphics cards. Merging grains form misfit dislocations.
© Robert Spatschek, Max-Planck-Institut für Eisenforschung GmbH