Strain induced Cementite decomposition
In order to investigate the thermodynamic driving force for the experimentally observed accumulation of C in ferritic layers of severely plastically deformed pearlitic wires, the stability of C intersitials in ferrite and of C vacancies in cementite are investigated as a function of uni-axial strain, using density-functional theory. In the presence of an applied strain, the C interstitial in ferrite is significantly stabilised, while the C vacancy in cementite is moderately destabilised by the corresponding strain states in cementite. The enhanced stabilisation of the C interstitial gives rise to an increase in the C concentration within the ferritic layers by up to two orders of magnitude. Our results thus suggest that in addition to the generally assumed non-equilibrium, dislocation-based mechanism, there is also a strain-indued thermodynamic driving force for the experimentally observed accumulation of C in ferrite.
Motivation

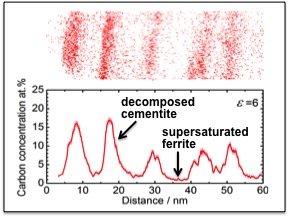
Cold-drawn pearlitic steel wires with the highest tensile strength among all metallic wires (6.3 Gpa [1-2]) have attracted a lot of attention in the last decade. Despite the fact that this nano-composite material has been subjected to numerous experimental and theoretical investigations, the origin of its extraordinary strength is still under debate. Only the recent developments in experimental characterization techniques reaching atomic and near atomic resolution (atom probe tomography, APT, and high resolution transmission electron microscopy, HR-TEM) provide sufficient information to advance our understanding of the involved complex phenomena. In this respect, APT studies reveal that the C concentration in bulk-like regions of ferrite can reach up to one atomic percent after wire drawing (Fig. 1). This value corresponds to an increase in the bulk C concentration by nine orders of magnitude, as compared to its equilibrium solubility at room temperature (10-5 ppm). In this work, we investigate the formation energy of C interstitials in α-Fe using DFT, as a function of the external loads applied during the wire drawing experiment. Moreover, in order to establish the thermodynamic driving force for the dissolution of cementite, the formation of C-vacancies in cementite is considered under corresponding strain conditions.
Methodology
The carbon formation energy as a function of applied strain is calculate by:

where EintFe-C is the total energy of bcc Fe with a C interstitial in a given strain state, EFe is the total energy of bulk iron in the same strain state, and µc is the C chemical potential. The stress dependent C vacancy formation energy is calculated using:

where EvacFe3C and EFe3C are the total energy of cementite in the presence and in the absence of a vacancy, respectively. The C chemical potential µC was set to the cohesive energy of C in the diamond structure. All total energies are calculated by means of the DFT method as implemented in the VASP code. Further, Bagaryatsky orientation relationships are used to couple the ferrite and cementite phases:

Results
The cementite and ferrite total energy in the presence and absence of defects are calculated as a function of applied strain along two directions parallel to the habit plane in the Bagaryatsky orientation relationship (see Fig.2).
In line with our expectation, the addition of C expands the bcc lattice in the direction of the two nearest neighbor Fe atoms around the C interstitial (see 1NN distance in Fig. 2a and d). Fig. 2b and e show that the ground state structure of the Fe-C system is shifted towards positive strains if the applied strain has components along the nearest neighbor direction. For example, for a C interstitial in the [100] direction (blue atom in Fig. 2a marked C[100]) and for a strain along [1-10] (red arrow in Fig. 2a) the shift of the equilibrium structure amounts to a positive strain of 0.013 (blue curve in Fig. 2b). A similar shift is found for a C atom in [100] and a strain along [111] (Fig. 2e). In the absence of strain components along the nearest neighbor direction, no energy can be gained by the application of the external strain. This is found for a C atom in the [001] direction and a strain along [1-10] (green curve in Fig. 2b).
Irrespective of which C site within the cementite matrix is considered, the C-vacancy is found to be destabilized by strains along either direction, as shown in Figs. 2c and f by the black arrows. The destabilization of the C vacancy can be understood by the reduced equilibrium volume of the cementite matrix in the presence of a C vacancy. Hence irrespective of the direction of the applied strain and the nature of the C site, the minimum energy configurations of the cementite vacancy system is found to be shifted towards negative strain states, which is why the external tensile load considered here induces a destabilization.
![Fig 2: (a,d) Schematics of the used geometries and (b,c,e,f) energetics as a function of strain. (a,b,c) correspond to strain along [1-10] in the ferrite and (d,e,f) to strain along [111] in the ferrite.](/3740104/original-1518437832.jpg?t=eyJ3aWR0aCI6MTM3OCwib2JqX2lkIjozNzQwMTA0fQ%3D%3D--ecb88f26f5ee275e5d63d16846bd508054fe1abd)
Voigt and Reuss limits
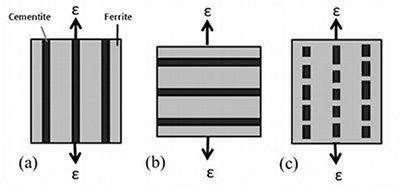
The microscopic results (Fig. 2) need to be homogenized in order to be related to the macroscopically observed strength. For that purpose, we consider the applied strain on the pearlitic lamellar structure within two extremes: the Voigt and the Reuss limits. The experimentally observed broken lamella after severe plastic deformation can be expected to have properties in between these two limits (see Fig.3).

Voigt limit
Within the Voigt limit, both phases experience the same strain which results in a reaction energy transferring a C atom from cementite to ferrite as:

The reaction energies for the above mentioned strain conditions (Fig. 2) are shown as a function of applied strain in Fig. 4.
![Fig 4: Calculated reaction energies of transferring a C atom from cementite to ferrite, as a function of strain along (a) [110]f and (b) [111]f in ferrite and the corresponding directions in cementite, as given by the Bagaryatsky orientation relationship. A constant strain state across the ferrite/cementite interface was assumed (Voigt limit).](/3740137/original-1518437833.jpg?t=eyJ3aWR0aCI6MTM3OCwib2JqX2lkIjozNzQwMTM3fQ%3D%3D--c07dc45915e71687303cb771e0440e4264b1093d)
Reuss limit
The equilibrium C concentration in ferrite as a function of applied strain, under a constant stress regime (Reuss limit), was found by first determining the strains within the two phases (εf and εcem) at a given stress (0 ≤ 6.3 GPa) using the stress-strain curves obtained from our DFT calculations. The strain states thus determined were used to calculate the corresponding formation energy of a C interstitial in ferrite and a C vacancy in cementite as described above. The macroscopic (external) strain state (εtot ) of the pearlite sample for a given stress state was found using

where vf and vcem are volume fractions of ferrite and cementite, respectively, which were taken to be 0.9 for ferrite and 0.1 for cementite, to account for the eutectoid composition of pearlite.
C concentration in ferrite
Knowing the reaction energy for a C atom transfer from ferrite to cementite and considering an ideal solution entropy, the C concentration in ferrite, Nint, and the vacancy concentration in cementite, Nvac, are obtained using the following equations:


A comparison of the equilibrium C concentration in ferrite under iso-strain and iso-stress conditions (Fig. 5) reveals an increased solubility in the Reuss limit. The difference to the Voigt limit stems from the independent deformation of the ferrite and cementite phases in the iso-stress model. Hence, due to its higher stiffness the cementite particles will deform less than the ferrite particles, resulting in a less pronounced destabilisation of the vacancy in cementite and a more pronounced stabilization of C in the ferrite.
Finally, considering the maximum equilibrium C concentration in ferrite particles within the pearlitic microstructure as a function of temperature (Fig. 5) suggests that the strain-induced enhancement is fairly temperature-independent in both the iso-strain and the iso-stress limit.
![Fig 5: Equilibrium carbon concentration in deformed (dashed lines) and undeformed (solid) ferrite layers within pearlitic structures of eutectic composition as a function of temperature. In (a) the applied strain is along [110] and in (b) along [111]. In the Voigt limit (green dashed line) an applied strain of 3% was assumed, while in the Reuss limit (red dashed) an external stress of 6 GPa.](/3740181/original-1518437834.jpg?t=eyJ3aWR0aCI6MTM3OCwib2JqX2lkIjozNzQwMTgxfQ%3D%3D--cf0952fafe0f710b06cc798f19ad9b941633a17b)
Conclusions
Our study allows to draw the following key conclusions [3]:
- The applied elastic strain stabilizes carbon in a ferrite octahedral site.
- The applied elastic strain destabilizes a vacancy in the cementite structure.
- The applied true elastic strain of 0.03 increases the C concentration in ferrite by 2 order of magnitude.
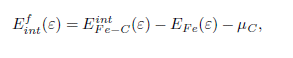
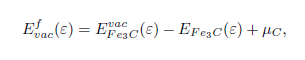
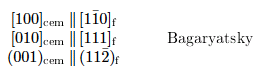
![Fig 2: (a,d) Schematics of the used geometries and (b,c,e,f) energetics as a function of strain. (a,b,c) correspond to strain along [1-10] in the ferrite and (d,e,f) to strain along [111] in the ferrite. Fig 2: (a,d) Schematics of the used geometries and (b,c,e,f) energetics as a function of strain. (a,b,c) correspond to strain along [1-10] in the ferrite and (d,e,f) to strain along [111] in the ferrite.](/3740104/original-1518437832.jpg?t=eyJ3aWR0aCI6ODQ4LCJmaWxlX2V4dGVuc2lvbiI6ImpwZyIsIm9ial9pZCI6Mzc0MDEwNH0%3D--479a5a17a2acd7b575fdb4438dce8f1df6e4c479)
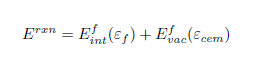
![Fig 4: Calculated reaction energies of transferring a C atom from cementite to ferrite, as a function of strain along (a) [110]f and (b) [111]f in ferrite and the corresponding directions in cementite, as given by the Bagaryatsky orientation relationship. A constant strain state across the ferrite/cementite interface was assumed (Voigt limit). Fig 4: Calculated reaction energies of transferring a C atom from cementite to ferrite, as a function of strain along (a) [110]f and (b) [111]f in ferrite and the corresponding directions in cementite, as given by the Bagaryatsky orientation relationship. A constant strain state across the ferrite/cementite interface was assumed (Voigt limit).](/3740137/original-1518437833.jpg?t=eyJ3aWR0aCI6ODQ4LCJmaWxlX2V4dGVuc2lvbiI6ImpwZyIsIm9ial9pZCI6Mzc0MDEzN30%3D--23de601c4d44807697558bda4a78839976c1b83b)
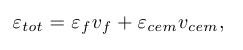
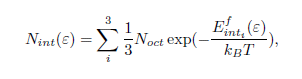
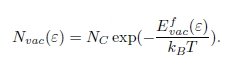
![Fig 5: Equilibrium carbon concentration in deformed (dashed lines) and undeformed (solid) ferrite layers within pearlitic structures of eutectic composition as a function of temperature. In (a) the applied strain is along [110] and in (b) along [111]. In the Voigt limit (green dashed line) an applied strain of 3% was assumed, while in the Reuss limit (red dashed) an external stress of 6 GPa. Fig 5: Equilibrium carbon concentration in deformed (dashed lines) and undeformed (solid) ferrite layers within pearlitic structures of eutectic composition as a function of temperature. In (a) the applied strain is along [110] and in (b) along [111]. In the Voigt limit (green dashed line) an applied strain of 3% was assumed, while in the Reuss limit (red dashed) an external stress of 6 GPa.](/3740181/original-1518437834.jpg?t=eyJ3aWR0aCI6ODQ4LCJmaWxlX2V4dGVuc2lvbiI6ImpwZyIsIm9ial9pZCI6Mzc0MDE4MX0%3D--179523e6c52660c8c041257b0d3136ddabee6fed)