Continuum modeling of fracture
Fracture is a fundamental mechanism of materials failure. Propagating cracks can exhibit a rich dynamical behavior controlled by a subtle interplay between microscopic failure processes in the crack tip region and macroscopic elasticity. Our modeling is mainly based on the phase field method, which is able to capture both the short-scale physics of failure and macroscopic linear elasticity within a self-consistent set of equations that can be simulated on experimentally relevant length and time scales.
Introduction
The dynamics of crack propagation is an important and long standing challenge in materials science and solid-state physics, and in the recent years the physics community saw a rebirth of interest in the problem of dynamic fracture, also in combination with the concept of phase field modeling. In this respect, fracture is yet another extension of a concept that was originally introduced to describe and simulate the kinetics of phase transitions - as the historical name phase field suggests. Today, this methodology has entered an "inflationary stage", and it has been successfully extended to various new applications in physics, materials science, but also biology and medicine. The characteristic property of phase field methods is the existence of one or more "phases", for example solid or liquid phases, which can be transformed into each other. While a scalar phase field was originally introduced to distinguish between different phases, other fields have been introduced to characterize other properties such as the local crystal orientation. On this broader scope, the phase field variables are therefore more appropriately denoted as order parameters. For the modeling of cracks, such an order parameter distinguishes between the solid phase and the "broken" state inside the crack. As usual in the phase field context, the order parameter changes smoothly between the states at the crack surfaces. The growth of a crack becomes then conceptually comparable to the front propagation in a first order phase transition. During the past years, several important questions concerning the growth of cracks have been successfully tackled by this new paradigm.
The uniform motion of a crack is relatively well understood in the framework of continuum theories. Here, the conventional approach is to treat the crack as a front or interface separating broken and unbroken regions of the material; propagation is governed by the balance of the elastic forces in the materials and cohesive stresses near the crack tip. Many characteristic features of crack propagation are nowadays well established by experimental studies. As soon as the flux of energy to the crack tip exceeds a critical value, the crack becomes unstable and starts to branch while emitting sound waves.
These phenomena are consistent with the continuum theory of sharp crack tips, but it fails to describe it, because the details of crack growth, in particular the chosen crack path and velocity, depend on details of cohesion on microscopic scales. Nevertheless, empirical energy balances and simple propagation laws that are frequently used in engineering applications, cannot account for the richness of actual fracture phenomena. In particular, they cannot predict dynamical instabilities of fast moving cracks. The fundamental mechanisms of those instabilities have been extremely difficult to elucidate because they appear to result from a non-trivial coupling between dynamical phenomena inside the crack tip region, known as process zone, and linear elasticity, with no clear separation of scale between atoms and the system size.
Large scale molecular dynamics (MD) simulations with about 107 atoms allowed to get deeper insights into the growth behavior of cracks. Although limited to submicron samples and very short timescales, these simulations were able to reproduce key features of crack propagation like the initial acceleration and the onset of instabilities. Nevertheless, a detailed understanding of the complex physics of crack propagation, in particular aspects of the pattern formation process, still remain a major challenge.
At this level, continuum descriptions, in particular phase field methods that avoid dynamical artifacts which are associated with the breaking of translational and rotational symmetry, offer a useful and complementary perspective on crack propagation as a pattern formation process.
Recent Results
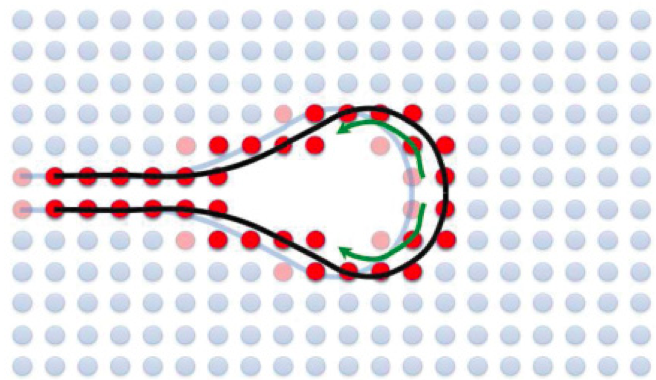
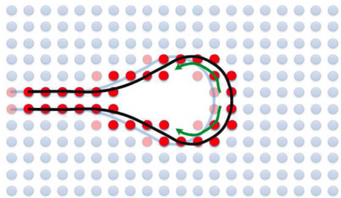
We have developed a continuum model of crack propagation in brittle viscoelastic materials. Thereby, the phenomenon of fracture is understood as an elastically induced non-equilibrium interfacial pattern formation process. In this spirit, a full description of a propagating crack provides the determination of the entire time dependent shape of the crack surface, which is assumed to be extended over a finite and self-consistently selected length scale. The mechanism of crack propagation, i.e. the motion of the crack surface, is then determined through linear non-equilibrium transport equations. Here, we have considered two different mechanisms, a first order phase transformation and surface diffusion. We have given scaling arguments showing that steady state solutions with a self-consistently selected propagation velocity and crack shape can exist provided that elastodynamic or viscoelastic effects are taken into account, whereas static elasticity alone is not sufficient. In this respect, inertial effects as well as viscous damping are identified to be sufficient crack tip selection mechanisms. Exploring the arising description of brittle fracture numerically, we study steady state crack propagation in the viscoelastic and inertia limit as well as in an intermediate regime, where both effects are important. The arising free boundary problems are solved by phase field methods and a sharp interface approach using a multipole expansion technique. Different types of loading, mode I, mode III fracture as well as mixtures of them, have been discussed.