Generation of optimal LCAO basis sets (QUAMOLs)
In this project, we explore the possibility to generate atomic orbital basis sets that optimally represent the electronic structure of a given material.
Motivation
From a macroscopic view, atoms are the building blocks of all matter, be it solids or molecules. It is therefore not surprising that the first electronic structure theories started from atoms, expressing electronic states as a Linear Combination of Atomic Orbitals, or LCAO. While it is nowadays established that the true atomic orbitals are a poor basis set for accurate calculations, the concept of atom-centered orbitals (sloppily called atomic orbitals) for the calculation and more importantly analysis of electronic structure has survived and bloomed. A huge variety of atomic orbital basis sets exists, ranging from Gaussians over Slater-Koster orbitals to numerical orbitals. It has become an art to choose the right atomic orbitals for a specific purpose. Our idea is to reverse this process: first, we perform calculations with a converged systematic basis (presently plane waves), and then we try to find atomic orbitals that reproduce the result optimally. By defining a proper measure of deviation, this gives us a systematic way of generating optimal atomic basis sets of predefined size for specific applications.
Change between atomic orbital & plane-wave representations
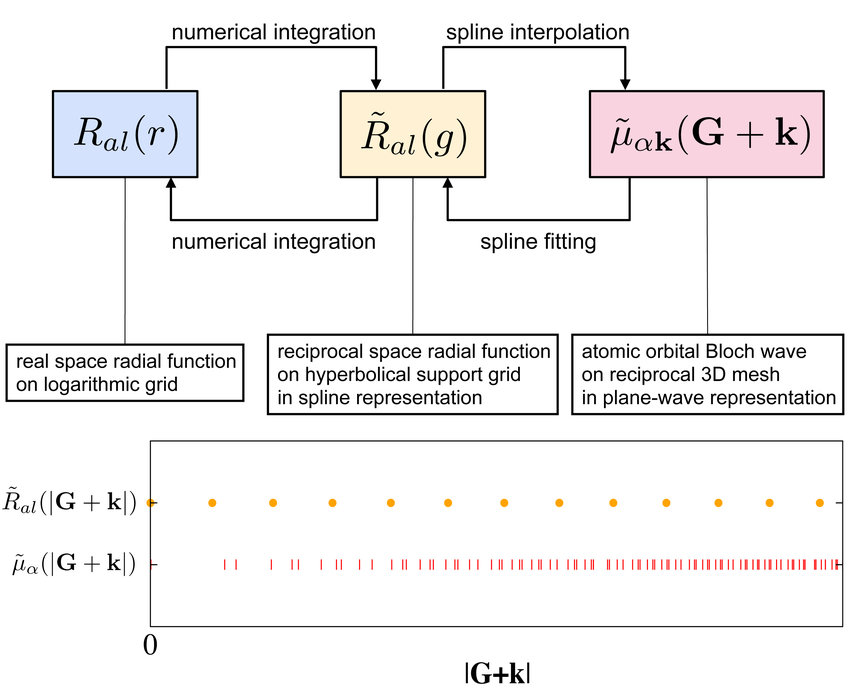
A first important step is to implement and test the transformation between the atomic orbital representation and the plane waves. Each atomic orbital |μ> is given on a radial grid and assigned a certain angular momentum symmetry (i.e. s, p, d, etc.). The transformation to plane waves is a standard task in plane-wave codes. The reverse transformation, i.e. from plane waves back to radial grids, has now been added. The introduction of a reciprocal radial support grid, and a continuous cubic spline function to interpolate between the support points, has two major advantages. On the one hand, it is an alternative, but fully equivalent representation of the radial shapes in real space. By focussing on the reciprocal space form, one avoids computational expensive numerical integrations for each 3D plane-wave coefficient. On the other hand, the more evenly distributed grid points cure the unbalanced distribution of the full G+k mesh for numerical integration, resulting in smoother radial shapes than a direct transformation from G+k to the real radial space would produce. The transformation from the huge number of G+k points to the even grid is done by least-square fitting.

Generating QUAMOLs by minimizing the Hilbert-space spillage
We have also defined a quality measure to be optimized: the Hilbert-space spillage of the bands |nk>, i.e.

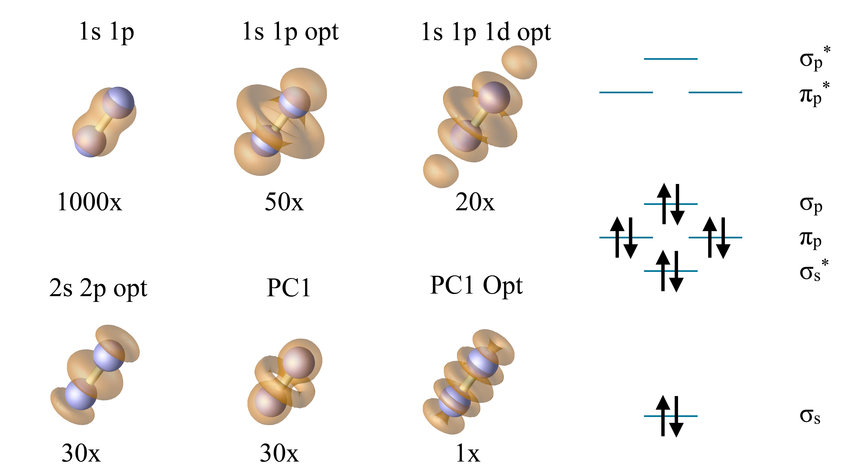
where wk denotes the k-point weights and fnk is a filtering factor to focus on such bands which are of interest. The projector Pk maps the band states |nk> given in their plane-wave representation onto the atomic orbital basis set. The Hilbert-space spillage can be understand as summed norm spillage due to the projection. If the atomic orbital basis were complete, the projected norm should be the same as in the plane-wave representation, but it is usually less. For example, using (pseudo)atomic s+p orbitals in N2 the deviation amounts to 4.7%. Optimizing the orbitals reduces the deviation to 1.0%, e.g., a factor of 5 better! We call them QUantitatively optimized AtoMic OrbitaLs, short: QUAMOLs. Introducing more basis functions ending up with two s, two p, and one d function (PC1) reduces the deviation already to 0.32% in the initial guess. The optimization procedure reduces the spillage further to only 0.0074%. The effects of this optimization can nicely be seen in the residual density plots which show that part of the Hilbert space which is poorly described, allowing a further improvement of the basis set.

Transferability

The transferability of a basis set is a crucial issue. Our aim is to provide basis set that do not describe the situation they are designed for optimally, but also give quantitatively good results when changing the chemical surroundings, i.e. atomic relaxation, introduction of defects in bulk systems, etc.
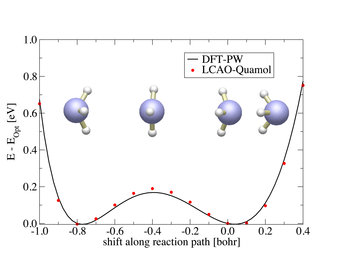
As a first test case we have checked how the QUAMOLs that were generated at the ideal ammonia structure, perform when modeling the NH<sub>3</sub> umbrella mode up to the molecular flip. This is shown in the graph below. The energy barrier for this flip differs by only 21 meV when comparing the QUAMOLs to the plane-wave basis set.
This gives rise to the assumption that our optimized atomic orbitals are flexible enough to accurately describe situations with a changing chemical environment. Next test systems will focus on the description of defects in supercells containing thousands of atoms.