Neue Mittel-Mangan-Stähle
Dirk Ponge*, Alisson Kwiatkowski da Silva
Max-Planck-Institut für Eisenforschung GmbH, 40237 Düsseldorf, Germany - *Kontaktdaten: ponge@mpie.de, +49-211-6792-438
Mittel-Mangan-Stähle (MMnS) ermöglichen hohe Festigkeit bei hoher Duktilität. Wegen des geringeren Mn-Gehaltes (4 − 12 % Massenanteil) sind MMnS kostengünstiger als Hoch-Mangan-Stähle (HMnS). Damit sind MMnS vielversprechende Kandidaten für die 3. Generation von hochfesten Automobilstählen. Aufgrund der Mehrphasigkeit bieten sie im Vergleich zu HMnS mehr Möglichkeiten, durch Wahl der Stahlzusammensetzung und Herstellparameter gezielt unterschiedliche Gefüge einzustellen, wie z.B. lamellare Gefüge (z.B. gegen Kurzzeitermüdung [1]) oder Gefüge mit gleichachsigem Ferrit und Austenit (z.B. für hohe Kerbschlagzähigkeit [2]). Über konventionelle Herstellprozesse wie z.B. Warmwalzen und interkritische Glühung können ultrafeinkörnige Gefüge mit Korngrößen unter 0,5 µm produziert werden, die bei anderen Stählen nur durch aufwendige Methoden mittels SPD (severe plastic deformation) möglich wären [3]. Durch die Vielseitigkeit der möglichen Gefüge und des komplizierten Verformungsverhaltens haben die mehrphasigen MMnS (typisch Ferrit/Austenit oder Martensit/Austenit) ein enormes Potenzial, das bisher nicht ausgeschöpft wurde. Das Design von Stahlzusammensetzung und Herstellparameter ist anspruchsvoll, da beides aufeinander abgestimmt werden muss.
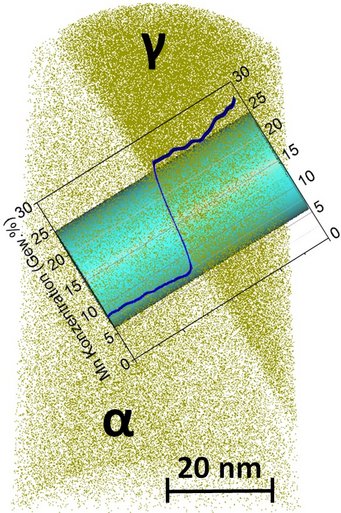
Mittels Gefügecharakterisierung in Kombination mit thermodynamischen und kinetischen Rechnungen hat sich das MPIE zunächst auf die Klärung der relevanten Mechanismen konzentriert. Ein Beispiel zeigt das Bild: Bei der interkritischen Glühung wächst sich neu bildender Austenit (γ) in den Martensit (α). Bereits beim Wachstum wird Mn umverteilt (partitioniert) und die Anreicherung im Austenit zum Erreichen der gewünschten Stabilität und Stapelfehlerenergie sichergestellt.
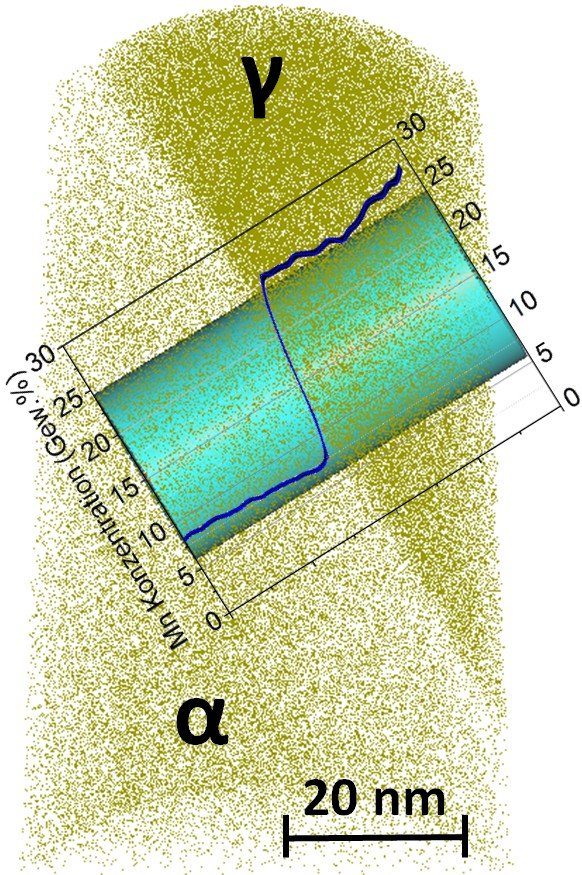
Atomsondenrekonstruktion eines Stahls mit 9 % Massenanteilen Mn
An der Phasengrenze α/γ besteht ein lokales Gleichgewicht. Dies führt dazu, dass der Austenit bereits nach der Keimbildungsphase mit der entsprechenden Gleichgewichtspartitionierung wächst. Diese hängt von der interkritischen Temperatur ab und kann durch thermodynamische Berechnung vorhergesagt werden. Aus der resultierenden Zusammensetzung des Austenits kann die Stapelfehlerenergie berechnet werden, die in einem bestimmten Bereich liegen muss, um den TRIP- und/oder TWIP-Effekt zu ermöglichen. Dies stellt die hohe Duktilität sicher.
Bei hoher interkritischer Temperatur rekristallisiert der Martensit zu gleichachsigem Ferrit und es bildet sich ein ebenfalls gleichachsiger Reversionsaustenit. Die Untersuchung der Verteilung der Dehnungen auf Ferrit und Austenit zeigt, dass zunächst der Ferrit als weichere Phase die plastische Verformung trägt. Aufgrund der niedrigen Verfestigung von Ferrit führt das zu ausgeprägter Streckgrenze und Lüdersdehnung. Bei steigender Dehnung verformt sich dann auch der Austenit und verzögert durch seine höhere Verfestigungsrate die Einschnürung.
Bei tiefer interkritischer Temperatur rekristallisiert der Martensit nicht. Austenit entsteht entlang aller Korngrenzen im Martensit und es entsteht die lamellare Morphologie. Da der Martensit nun fester ist als der Austenit, wird die Verformung bereits zu Beginn vom Austenit (höhere Verfestigung) bestimmt und es tritt keine ausgeprägte Streckgrenze auf.
Die Kenntnisse der Mechanismen erlaubt es, gezielter Zusammensetzung und Herstellparameter von MMnS zu entwickeln, um Gefüge mit gewünschten Eigenschaften einzustellen.
Literatur
[1] Koyama, M.; Zhang, Z.; Wang, M.; Ponge, D.; Raabe, D.; Tsuzaki, K.; Noguchi, H.; Tasan, C. C.: Science 355 (2017) Nr. 6329 S. 1055/3.
[2] Han, J.; Kwiatkowski da Silva, A.; Ponge, D.; Raabe, D.; Lee, S.-M.; Lee, Y.-K.; Lee, S.-I.; Hwang, B.: Acta Mat. 122 (2017), S. 199/208.
[3] Song, R.; Ponge, D.; Raabe, D.; Speer, J. G.; Matlock, D. K.: Mat. Sci. Eng. A 441 (2006), Nr. 1−2, S. 1/17.