Quantenmechanisch geführtes Design von TWIP Stählen

Ab-initio-basierte Multiskalensimulationsmethoden ermöglichen die Vorhersage grundlegender Deformationsmechanismen in komplexen Materialien als Funktion der Legierungszusammensetzung und Prozessparameter. Für Hoch-Mn-Stähle, die Festigkeiten von über 1 GPa und bis zu 70% Dehnung erzielen, wird die Leistungsfähigkeit dieser neuen Methoden gezeigt.

Tilmann Hickel*, Franz Roters, Dierk Raabe und Jörg Neugebauer

Max-Planck-Institut für Eisenforschung GmbH, 40237 Düsseldorf, Germany - *Kontaktdaten: t.hickel@mpie.de, +49-211-6792-397

Das Verformungsverhalten moderner Stähle hängt entscheidend von elementaren Prozessen auf der Ebene der Atome ab. In TWIP-Stählen sorgt die Ausbildung von Zwillingsgrenzen für eine Reduktion der Versetzungsbeweglichkeit und damit für eine Verfestigung des Materials (TWIP: Twinning Induced Plasticity). Mit Ab-initio-Simulationsmethoden, die auf quantenmechanischen Gesetzen beruhen (ab initio: von den Grundlagen), können die zugrunde liegenden Mechanismen am Computer untersucht werden, ohne auf experimentellen Input oder empirische Materialgesetze angewiesen zu sein. Auf diese Weise gelingt es zum Beispiel, die richtige Materialzusammensetzung einzustellen, um den Verfestigungsvorgang zu verbessern.

Für ein solches Materialdesign hat sich die Stapelfehlerenergie (SFE) als idealer Kontrollparameter herausgestellt [1]. Damit sich in den TWIP-Stählen die zur Verfestigung benötigten Zwillingsgrenzen ausbilden, müssen die atomaren Ebenen im Material verschoben werden. Die SFE gibt an, wie viel Energie aufzuwenden ist, um einen solchen Stapelfehler zu bilden. Die SFE kann ab initio berechnet werden und erlaubt damit, das mechanische Verhalten eines Bauteils aus TWIP-Stahl alleine am Computer zu bestimmen [2].

Am Max-Planck-Institut für Eisenforschung (MPIE) wurden dazu in den letzten Jahren durch Kombination der Dichtefunktionaltheorie (DFT) und der statistischen Thermodynamik neue Ab- initio-Simulationsprogramme entwickelt [3], die die Abhängigkeiten der SFE von den relevanten Prozessparametern, insbesondere aber auch von der chemischen Legierungszusammensetzung präzise vorhersagen.

So konnte nicht nur ermittelt werden, dass ein Mn-Gehalt von ca. 20% einen besonders niedrigen SFE-Wert ergibt und so zu einer hohen Materialfestigkeit führt. Es konnte auch erklärt werden, warum verschiedene experimentelle Studien zu ganz unterschiedlichen Aussagen über den Einfluss von Kohlenstoff auf die SFE gekommen sind [4]: Verformt man einen TWIP-Stahl bei Raumtemperatur, sind die Kohlenstoffatome kaum beweglich und verbleiben in der Nähe des Stapelfehlers. Bei einer Wärmebehandlung verlassen sie hingegen die energetisch ungünstigen Positionen in der Stapelfehlerregion und verändern dadurch den Wert der SFE.

Unter Berücksichtigung auch von weiteren mikroskopischen Einflüsse wie lokalen Spannungen, Magnetismus und Gitterschwingungen konnte am MPIE ein Plastizitätsmodell entwickelt werden [5], das für einen festen Satz physikalischer Parameter die akkurate Vorhersage der Spannungs-Dehnungs-Kurven bei allen für eine Prozessierung relevanten Temperaturen erlaubt. Die Simulation der Verformung einer Crashbox zeigt, dass mit diesen Simulationstools das Verhalten von komplexen Komponenten aus TWIP-Stählen unter Realbedingungen korrekt vorhergesagt wird [2].

Dieses Design-Konzept ist im Rahmen eines Forschungsverbunds (Sonderforschungsbereich SFB761) mit der RWTH Aachen unter dem Namen „Stahl – ab initio“ entstanden. Der Verbund hat so erfolgreich gearbeitet, dass die Deutsche Forschungsgemeinschaft auch die Finanzierung einer dritten Projektphase bis 2019 bewilligt hat. Sie wird genutzt, um Mn-basierte TWIP-Stähle mithilfe der Quantenmechanik für den Einsatz in der Automobilindustrie zu optimieren.

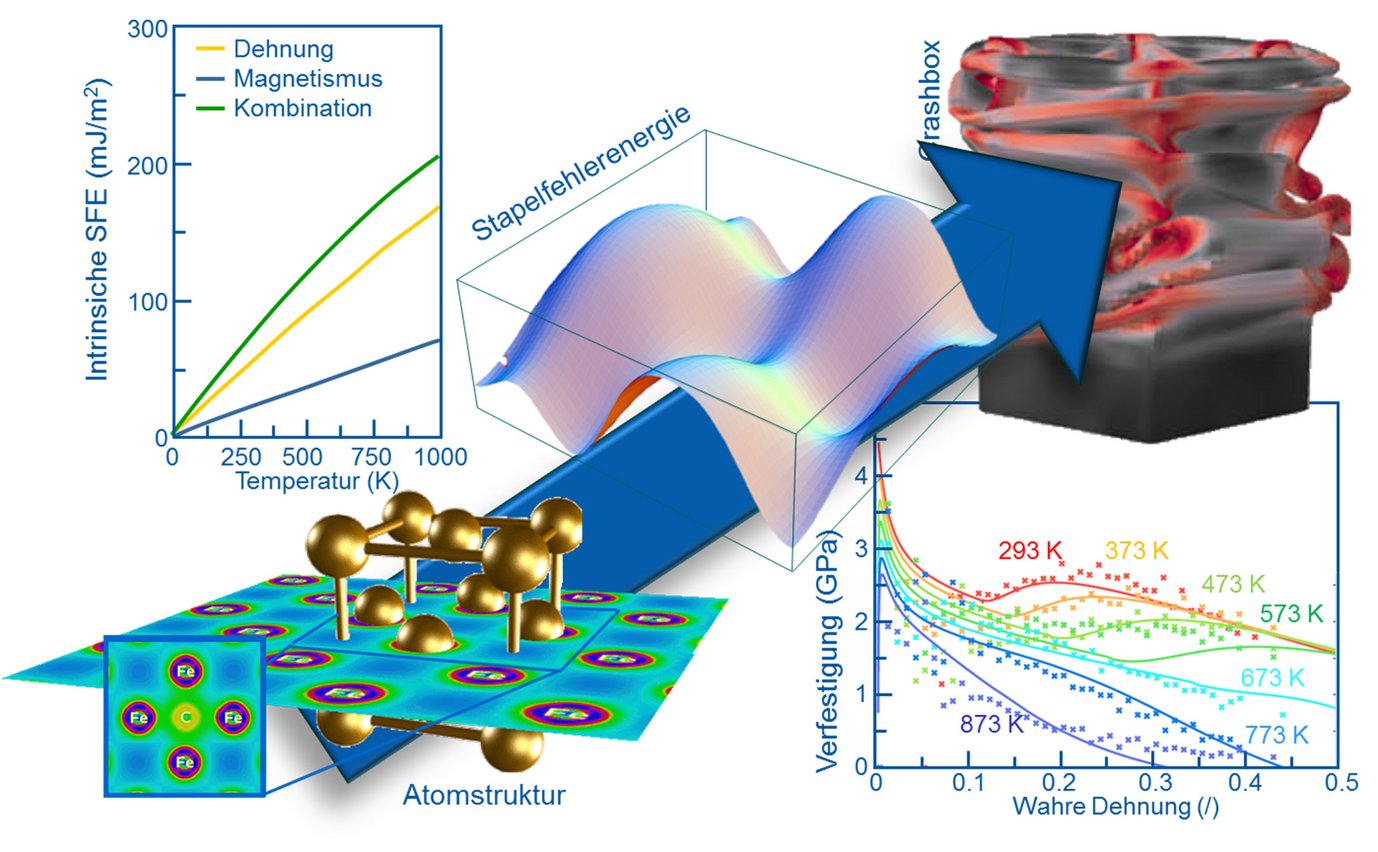
Einsatz von ab-initio-Methoden zur Beschreibung des Verhaltens von TWIP- Stählen auf der Bauteilebene bei verschiedenen Temperaturen. Die Stapelfehlerenergie ist dafür von zentraler Bedeutung

www.stahlundeisen.de

Einsatz von ab-initio-Methoden zur Beschreibung des Verhaltens von TWIP- Stählen auf der Bauteilebene bei verschiedenen Temperaturen. Die Stapelfehlerenergie ist dafür von zentraler Bedeutung

www.stahlundeisen.de

Literatur:

[1] Raabe, D.; Roters, F., Neugebauer, J.; Gutierrez-Urrutia, I.; Hickel, T.; Bleck, W.; Schneider, J.M.; Wittig, J.E.; Mayer, J.: MRS Bulletin 41 (2016), S.320/25.

[2] Güvenç,O.; Roters, F.; Hickel, T.; Bambach, M.: JOM 67 (2015), S.120/28.

[3] Hickel, T.M; Grabowski, B.; Körmann, F.; Neugebauer, J.; Phys, J.: Cond. Mat. 24 (2011), 053202.

[4] Hickel, T.; Sandlöbes, S.; Marceau, R.K.W.; Dick, A.; Bleskov, I.; Neugebauer, J.; Raabe, D.: Acta Mater. 75 (2014), S. 147/55.

[5] Steinmetz, D.R.; Jäpel, T.; Wietbrock, B.; Eisenlohr, P.; Gutierrez-Urrutia, I.; Saeed–Akbari, A.; Hickel, T.; Roters, F.; Raabe, D.: Acta Mat. 61 (2013), S.494.